Trigonometriset funktiot
Muuta asteiksi
a) \(1 \text{ rad}\)
b) \(\dfrac{\pi}{3} \text{ rad}\)
c) \(\frac{1}{8}\text{ rad}\)
d) \(25^{\circ}\)
e) \(45^{\circ}\)
f) \(60^{\circ}\)
a)
\(\pi \text{ rad} = 180^{\circ} \qquad ||:\pi\)
\(1 \text{ rad} = \dfrac{180^{\circ}}{\pi} \) \(\quad \color{red}{\text{(+0,5p)}}\)
\(1 \text{ rad} \approx 57,3^{\circ}\) \(\quad \color{red}{\text{(+0,5p)}}\)
b)
\(1 \text{ rad} = \dfrac{180^{\circ}}{\pi} \qquad ||:8\)
\(\dfrac{1}{8} \text{ rad} = \dfrac{180^{\circ}}{8\pi} \qquad\)
\(\dfrac{1}{8} \text{ rad} = \dfrac{45^{\circ}}{2\pi} \qquad\) \(\quad \color{red}{\text{(+0,5p)}}\)
\(\dfrac{1}{8} \text{ rad} \approx 7,2^{\circ}\) \(\quad \color{red}{\text{(+0,5p)}}\)
c)
\(\pi \text{ rad} = 180^{\circ} \qquad ||:3\)
\(\dfrac{\pi}{3} \text{ rad} = 60^{\circ}\) \(\quad \color{red}{\text{(+1p)}}\)
d)
\(180^{\circ} =\pi \text{ rad} \ \ \qquad ||:180\)
\(1^{\circ} =\dfrac{\pi}{180} \text{ rad} \qquad ||\cdot 25\)
\(25^{\circ} =\dfrac{25\pi}{180} \text{ rad}\)
\(25^{\circ} =\dfrac{5\pi}{36}\ \text{ rad}\) \(\quad \color{red}{\text{(+1p)}}\)
e)
\(1^{\circ} =\dfrac{\pi}{180} \text{ rad} \qquad ||\cdot 45\)
\(45^{\circ} =\dfrac{45\pi}{180} \text{ rad} \)
\(45^{\circ} =\dfrac{\pi}{4} \text{ rad} \) \(\quad \color{red}{\text{(+1p)}}\)
f)
\(1^{\circ} =\dfrac{\pi}{180} \text{ rad} \qquad ||\cdot 60\)
\(60^{\circ} =\dfrac{60\pi}{180} \text{ rad} \)
\(60^{\circ} =\dfrac{\pi}{3} \text{ rad} \) \(\quad \color{red}{\text{(+1p)}}\)
Määritä yksikköympyrän avulla
a) \(\sin 30^{\circ}\)
b) \(\cos 120^{\circ}\)
c) \(\tan 60^{\circ}\)
Suorakulmaisesta kolmiosta huomataan, että
\(\sin \alpha = \dfrac{y}{1}=y\)
\(\cos \alpha = \dfrac{x}{1}=x\)
\(\tan \alpha = \dfrac{y}{x}\)
a) Piirretään 30 astetta vastaava keskuskulma ja
tätä kulmaa vastaava kehäpiste P ympyrän kehälle. \(\quad \color{red}{\text{(+1p)}}\)
Yksikköympyrästä huomataan, että
\(\sin 30^{\circ} \approx 0,50\) \(\quad \color{red}{\text{(+1p)}}\)
b) Piirretään 120 astetta vastaava keskuskulma ja
tätä kulmaa vastaava kehäpiste P ympyrän kehälle. \(\quad \color{red}{\text{(+1p)}}\)
Yksikköympyrästä huomataan, että
\(\cos 120^{\circ} \approx -0,50\) \(\quad \color{red}{\text{(+1p)}}\)
c) Piirretään 120 astetta vastaava keskuskulma ja
tätä kulmaa vastaava kehäpiste P ympyrän kehälle.
Yksikköympyrästä huomataan, että
\(\cos 60^{\circ} \approx 0,50\)
\(\sin 60^{\circ} \approx 0,85\)
\(\tan 60^{\circ}=\dfrac{y}{x}\) \(\quad \color{red}{\text{(+0,5p)}}\)
\(\tan 60^{\circ} \approx \dfrac{0,85}{0,50}\) \(\quad \color{red}{\text{(+0,5p)}}\)
\(\tan 60^{\circ} \approx 1,7\) \(\quad \color{red}{\text{(+1p)}}\)
a) Määritä kuvaajasta funktion f jakson pituus. (2p)
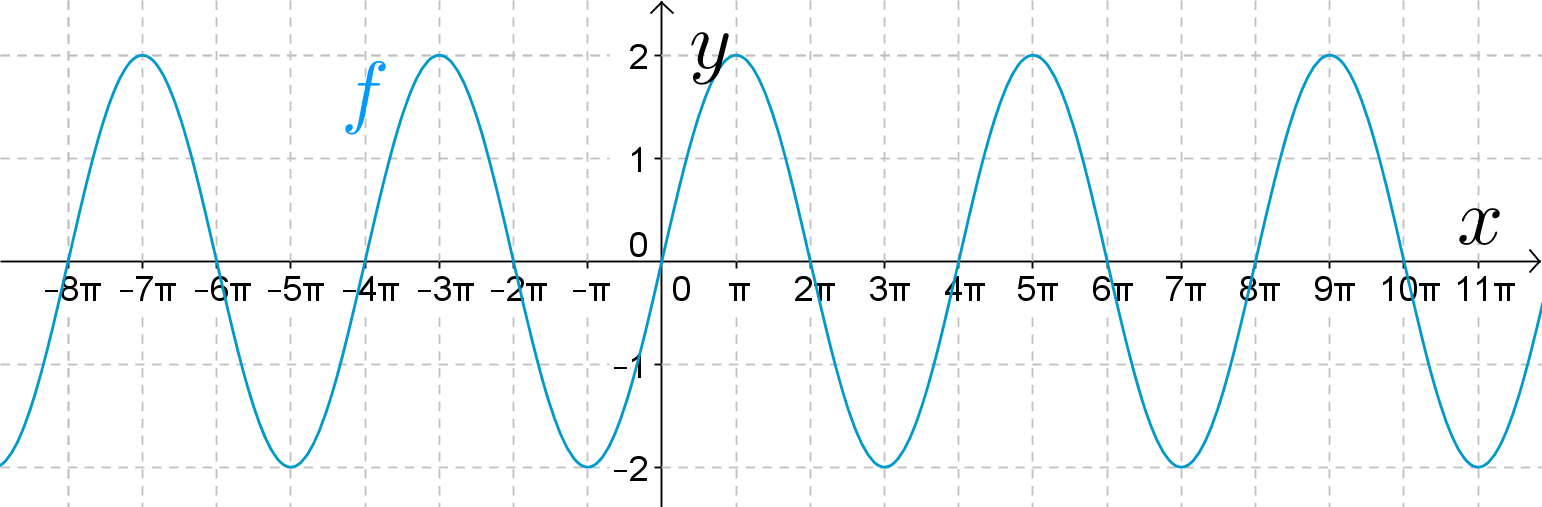
b) Mikä on lausekkeen \(2-5 \sin x\) pienin arvo? Entä suurin arvo? (4p)
a)
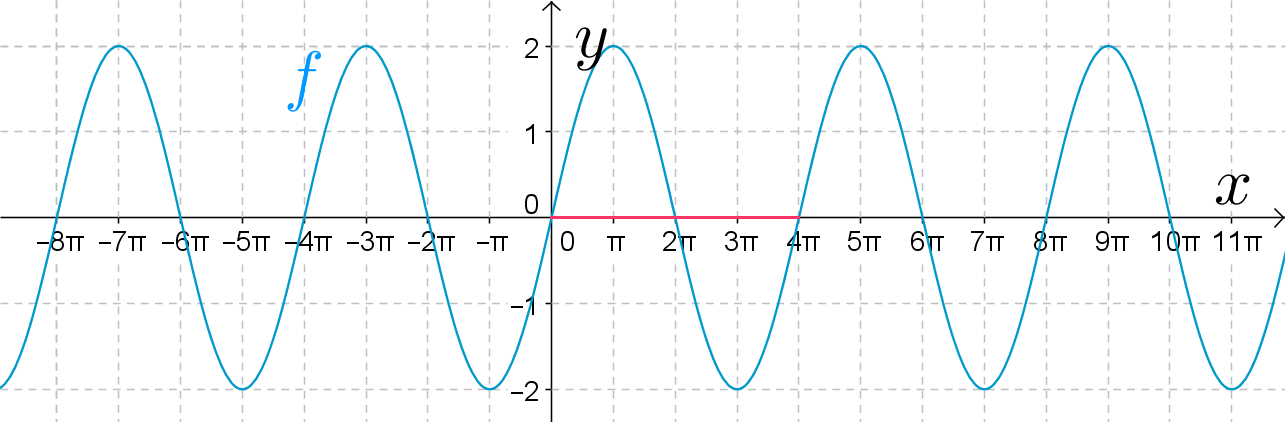
Kuvaajasta huomataan, että funktion jakso on noin \(4 \pi\). \(\quad \color{red}{\text{(+2p)}}\)
b) Sinin pienin arvo on -1 ja suurin arvo on 1.
\(-1 \leq \sin x \leq 1 \) \(\quad \color{red}{\text{(+1p)}}\)
\(-5 \leq -5\sin x \leq 5\) \(\quad \color{red}{\text{(+1p)}}\)
\(2-5 \leq 2-5\sin x \leq 2+5\)
\(-3 \leq 2-5\sin x \leq 7\) \(\quad \color{red}{\text{(+1p)}}\)
Vastaus: Lausekkeen \(2-5\sin x \) pienin arvo on -3 ja suurin arvo 7. \(\quad \color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
