Osoita, että kolmiot ovat yhdenmuotoisia.
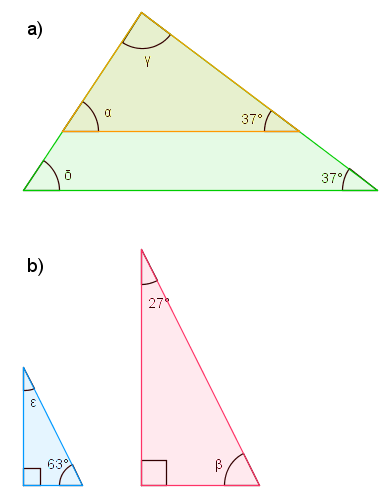
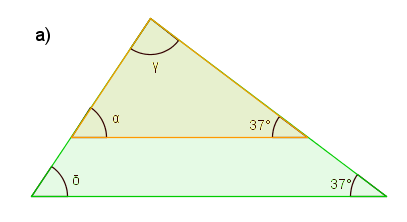
Molemmissa kolmioissa on $37$ asteen kulmat ja kulma $\gamma$ on yhteinen molemmille kolmioille $\color{Red}{(+1\text{p})}$, joten kaksi kulmaa -lauseen nojalla kolmiot ovat yhdenmuotoisia $\color{Red}{(+1\text{p})}$.
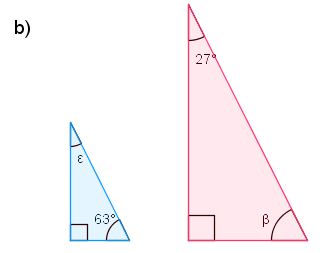
Lasketaan kulman $\epsilon$ suuruus:
$\epsilon = 180^o - (90^o + 63^o) = 27^o$ $\color{Red}{(+1\text{p})}$
Sinisen kolmion kulma $\epsilon$ on siis yhtä suuri kuin sen vastin kulma punaisessa kolmiossa $\color{Red}{(+1\text{p})}$. Tämän lisäksi molemmat kolmiot ovat suorakulmaisia $\color{Red}{(+1\text{p})}$, joten kaksi kulmaa -lauseen nojalla kolmiot ovat yhdenmuotoiset $\color{Red}{(+1\text{p})}$.
Laske janan $x$ pituus.
Pieni ja iso kolmio ovat keskenään yhdenmuotoisia, koska huippukulma on yhteinen ja pienen kolmion kantakulmat ovat samankohtaisia kulmia ison kolmion kantakulmien kanssa. $\color{Red}{(+1\text{p})}$
Kolmioissa vastinsivuja ovat sivut, joiden pituudet ovat $2$ ja $6$, sekä sivut, joiden pituudet ovat $2\sqrt{2}$ ja $x+2\sqrt{2}$ $\color{Red}{(+1\text{p})} $
TAPA 1:
Kolmioiden mittakaava on $1:3$, joten $\text{isomman kolmion sivu} = 3 \cdot \text{pienemmän kolmion sivu}$ $\color{Red}{(+1\text{p})} $
\(\begin{align} x+2\sqrt{2} &=3\cdot 2\sqrt{2} &&\color{Red}{(+1\text{p})} \\ x+2\sqrt{2} &=6\sqrt{2} && ||-2\sqrt{2} \\ x&= 6\sqrt{2} - 2\sqrt{2} \\ x&=4\sqrt{2} && \color{Red}{(+1\text{p})} \end{align}\)
TAPA 2:
Muodostetaan vastinsivujen suhteet:
\(\begin{align} \frac{2}{6}&=\frac{2\sqrt{2}}{x+2\sqrt{2}}& & \color{Red}{(+1\text{p})} \\ 2(x+2\sqrt{2}) &=6\cdot 2\sqrt{2} &||:2 & \color{Red}{(+1\text{p})}\\ x+2\sqrt{2} &=3\cdot 2\sqrt{2} \\ x&= 6\sqrt{2} - 2\sqrt{2} \\ &=4\sqrt{2} && \color{Red}{(+1\text{p})} \end{align}\)
Vastaus: $4\sqrt{2}$ $\color{Red}{(+1\text{p})}$
Kartan mittakaava on 1 : 20 000.
a) Koulu sijaitsee kartalla $3,\!6$ senttimetrin päässä kaupasta. Kuinka pitkä kävelymatka koululta on kauppaan?
b) Maijan koti sijaitsee $12,\!5$ kilometrin päässä koululta. Kuinka pitkä matka tämä on kartalla?
c) Hampurin ja Berliinin välinen etäisyys on linnuntietä 256 km. Kartalta mitattuna tämä etäisyys on 8 cm. Mikä on kartan mittakaava?
Mittakaava 1 : 20 000 tarkoittaa, että yksi senttimetri kartalla vastaa 20 000 senttimetriä eli 200 metriä luonnossa.
a) $3,\!6 \cdot 20\text{ }000 = 72 \text{ }000$ $\color{Red}{(+1\text{p})}$
$72 \text{ }000 \text{ cm}=720 \text{ m}$
Vastaus: Koulu sijaitsee 720 metrin päässä kaupasta $\color{Red}{(+1\text{p})}$
b) $12,\!5 \text{ km} = 1\text{ }250\text{ }000 \text{ cm}$
$\frac{1\text{ }250\text{ }000}{20\text{ }000}=62,\!5$ $\color{Red}{(+1\text{p})}$
Vastaus: Maijan kodin etäisyys koulusta on kartalla 62,5 senttimetriä $\color{Red}{(+1\text{p})}$
c) 8 cm kartalla on 256 km = 256 000 m = 25 600 000 cm luonnossa eli
\(\begin{align} \frac{25 \text{ }600 \text{ } 000}{8}=3\text{ }200\text{ }000 \end{align}\) $\color{Red}{(+1\text{p})}$
Vastaus: kartan mittakaava on $1:3\text{ } 200 \text{ }000$ $\color{Red}{(+1\text{p})}$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
