Suorakulmaisen kolmion toisen kateetin pituus on 6 ja hypotenuusan pituus on 10. Laske puuttuvan kateetin pituus ja kolmion pinta-ala.

Pythagoraan lauseella
\(\begin{align} 6^2+x^2&=10^2 & & \color{Red}{(+1\text{p})}\\ x^2 &= 100 - 36 & & \color{Red}{(+1\text{p})}\\ x^2&= 64 &||\sqrt{ } & \\ x&=\pm 8 && \color{Red}{(+1\text{p})} \end{align}\)
Pituus ei voi olla negatiivista $\color{Red}{(+1\text{p})}$, joten puuttuvan kateetin pituus on 8.
\(\begin{align} A&=\frac{6\cdot 8}{2} & \color{Red}{(+1\text{p})}\\ &=24 & \color{Red}{(+1\text{p})} \end{align}\)
Vastaus: puuttuvan kateetin pituus on 8 ja kolmion pinta-ala on 24
Onko kolmio suorakulmainen?
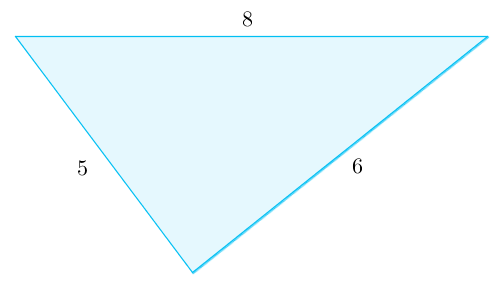
Jos kolmio on suorakulmainen, niin kolmion sivujen pituudet toteuttavat Pythagoraan lauseen $a^2+b^2=c^2$. $\color{Red}{(+2\text{p})}$
Hypotenuusa on pisin sivu eli $c=8$ ja kateetit ovat $a=5$ ja $b=6$.
Tarkistetaan, toteutuuko Pythagoraan lause:
\(\begin{align} &a^2+b^2 \\ =&5^2+6^2 \\ =&25+36 \\ =&61 &\color{Red}{(+1\text{p})} \end{align}\)
\(\begin{align} &c^2 \\ =& 8^2 \\ =& 64 &\color{Red}{(+1\text{p})} \end{align}\)
Koska $61 \neq 64$, niin Pythagoraan lause ei toteudu, joten kolmio ei ole suorakulmainen. $\color{Red}{(+1\text{p})}$
Vastaus: Kolmio ei ole suorakulmainen
Ratkaise kolmion sivujen pituudet kahden desimaalin tarkkuudella sekä kulmien suuruudet asteen tarkkuudella

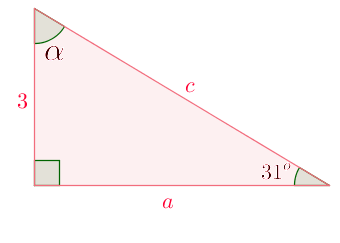
Kolmion kulmien summa on $180^o$, joten puuttuvan kulman suuruus saadaan
$\alpha= 180^o - 90^o - 31^o=59^o$. $\color{Red}{(+1\text{p})}$
Ratkaistaan kolmion puuttuva kateetti tangentin avulla:
\(\begin{align} \tan 31^o&=\frac{3}{a}&&||\cdot a & \color{Red}{(+1\text{p})} \\ a \cdot \tan 31^o &= 3& &||: \tan 31^o \\ a &= \frac{3}{\tan 31^o} \\ &=4,\!9928...&& & \color{Red}{(+1\text{p})} \\ & \approx 4,\!99 \end{align}\)
Ratkaistaan kolmion hypotenuusa sinin avulla:
\(\begin{align} \sin 31^o&=\frac{3}{c}&&||\cdot c & \color{Red}{(+1\text{p})} \\ c \cdot \sin 31^o &= 3& &||: \tan 31^o \\ x &= \frac{3}{\sin 31^o} \\ &=5,\!8248...&& & \color{Red}{(+1\text{p})} \\ & \approx 5,\!82 \end{align}\)
Vastaus: Kolmion kulmien suuruudet ovat $90^o$, $31^o$ ja $59^o$. Kolmion sivujen pituudet ovat $3.00$, $4.99$ ja $5.82$. $\color{Red}{(+1\text{p})}$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
