Suorakulmaisen särmiön muotoisen kannellisen laatikon mitat ovat 25 cm x 30 cm x 20 cm.
a) Aiot maalata laatikon ulkopuolelta. Laske tätä varten laatikon pinta-ala.
b) Laske, kuinka monta litraa jauhoja laatikkoon mahtuu.
a) Suorakulmainen särmiö koostuu kuudesta suorakulmiosta, joista vastakkaiset tahkot ovat aina yhtä suuria. Siten laatikon pinta-ala saadaan
\(\begin{align} A&=2\cdot 25\cdot 30 + 2\cdot 25\cdot 20 + 2\cdot 20 \cdot 30 & \color{Red}{(+1\text{p})}\\ &= 3700 \end{align}\)
Vastaus: 3700 cm$^2$ $\color{Red}{(+1\text{p})}$
b) Suorakulmaisen särmiön tilavuus saadaan
\(\begin{align} V&=A_p\cdot h &\color{Red}{(+1\text{p})}\\ &= 25\cdot 30 \cdot 20 \\ &= 15 \text{ } 000 &\color{Red}{(+1\text{p})} \end{align}\)
$15 \text{ } 000 \text{ cm}^3 = 15 \text{ dm}^3 = 15 \text{ } l$ $\color{Red}{(+1\text{p})}$
Vastaus: 15 litraa $\color{Red}{(+1\text{p})}$
Kappaleen pohja on ympyrä, jonka säde on 12,0 cm ja sen korkeus on 27,0 cm. Laske kappaleen tilavuus, kun
a) se on lieriö.
b) se on kartio.
a) Lieriön tilavuus lasketaan
\(\begin{align} V&=A_p\cdot h \\ &= \pi r^2 \cdot27,\!0 & \color{Red}{(+1\text{p})}\\ &= \pi \cdot (12,\!0)^2\cdot 27,\!0 \\ &= 3888\pi \\ &= 12 \text{ } 214,\!512... &\color{Red}{(+1\text{p})} \end{align}\)
Vastaus: Lieriön tilavuus on 12 200 cm$^3$ $\color{Red}{(+1\text{p})}$
b) Kartion tilavuus lasketaan
\(\begin{align} V&=\frac{1}{3}A_p \cdot h \\ &= \frac{1}{3}\cdot \pi r^2\cdot 27,\!0 &\color{Red}{(+1\text{p})}\\ &= \frac{1}{3}\cdot \pi \cdot (12,\!0)^2\cdot 27,\!0 \\ &= 1296\pi \\ &= 4071,\!504... &\color{Red}{(+1\text{p})} \end{align}\)
Vastaus: Kartion tilavuus on 4070 cm$^3$
Suoran kartion korkeus on 3 ja neliönmuotoisen pohjan sivun pituus 2. Laske kartion vaipan pinta-ala.
Kartion vaippa koostuu neljästä tasakylkisestä kolmiosta, joiden kannan pituus on $2$ ja korkeus on $s$ $\color{Red}{(+1\text{p})}$:
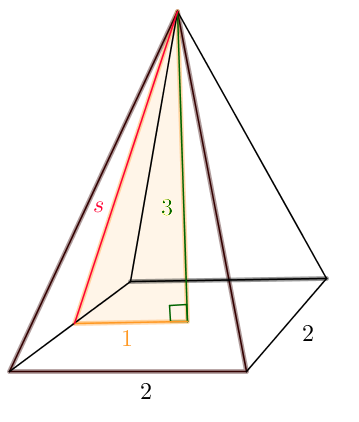
Sivujanan $s$ pituus saadaan ratkaistua Pythagoraan lauseella:
\(\begin{align} 1^2+3^2&=s^2 \\ 1+9&=s^2 &||\sqrt{} \\ s &= \pm \sqrt{10} &&\color{Red}{(+1\text{p})} \end{align}\)
Pituus ei voi olla negatiivista, joten sivujanan $s$ pituus on $\sqrt{10} \color{Red}{(+1\text{p})}$.
Lasketaan nyt pyramidin vaipan muodostavien kolmioiden pinta-ala:
$A_\text{kolmio}=\frac{2\cdot \sqrt{10}}{2}=\sqrt{10} \color{Red}{(+1\text{p})}$,
joten pyramidin vaipan pinta-ala on
$A_v = 4\cdot A_\text{kolmio}= 4\cdot \sqrt{10} = 4\sqrt{10}\color{Red}{(+1\text{p})}$
Vastaus: Kartion vaipan pinta-ala on $4\sqrt{10}$ $\color{Red}{(+1\text{p})}$
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
