Piirrä vektori \(\overline{a}+\overline{b}-\overline{c}\)
Vektori \(-\overline{c}\) on vektorin \(\overline{c}\) vastavektori.
Vektorin vastavektorilla on sama pituus, mutta
vastavektorin suunta on alkuperäiselle vektorille vastakkainen.
Vektorisumma saadaan piirrettyä piirtämällä
vektorit \(\overline{a}, \ \overline{b} \text{ ja } -\overline{c}\) peräkkäin..
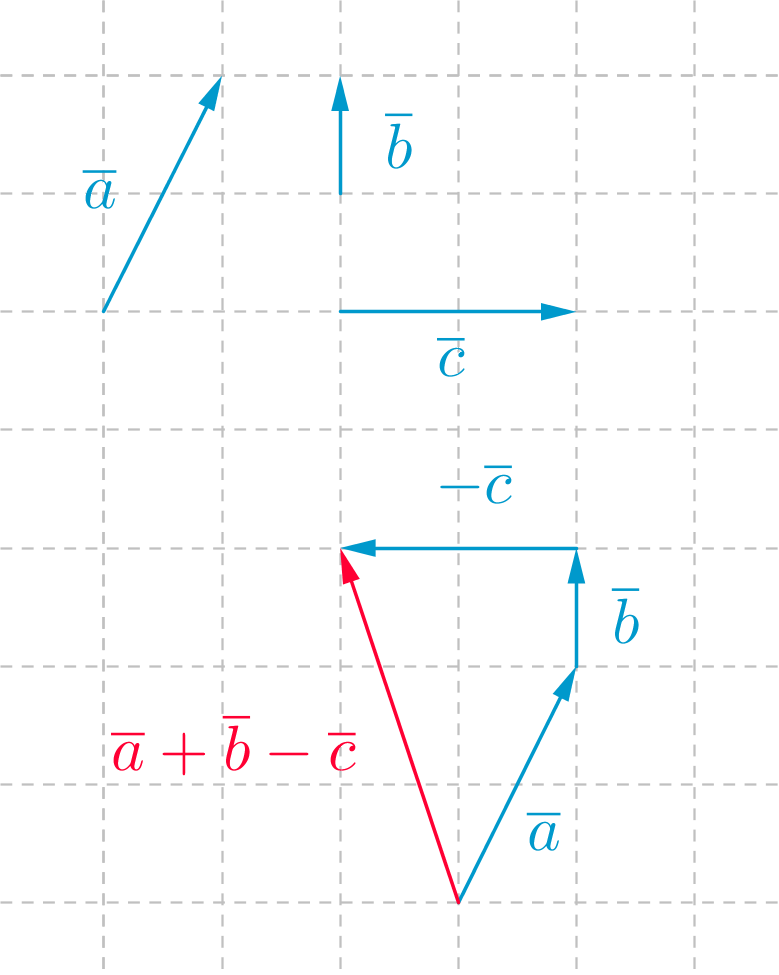
\(\quad \color{red}{\text{(Kuva oikein +6p)}}\)
Määritä vektorien
a) \(\overline{a} \text{ ja } \overline{b}\)
b) \(\overline{b} \text{ ja } \overline{c}\)
välinen kulma.
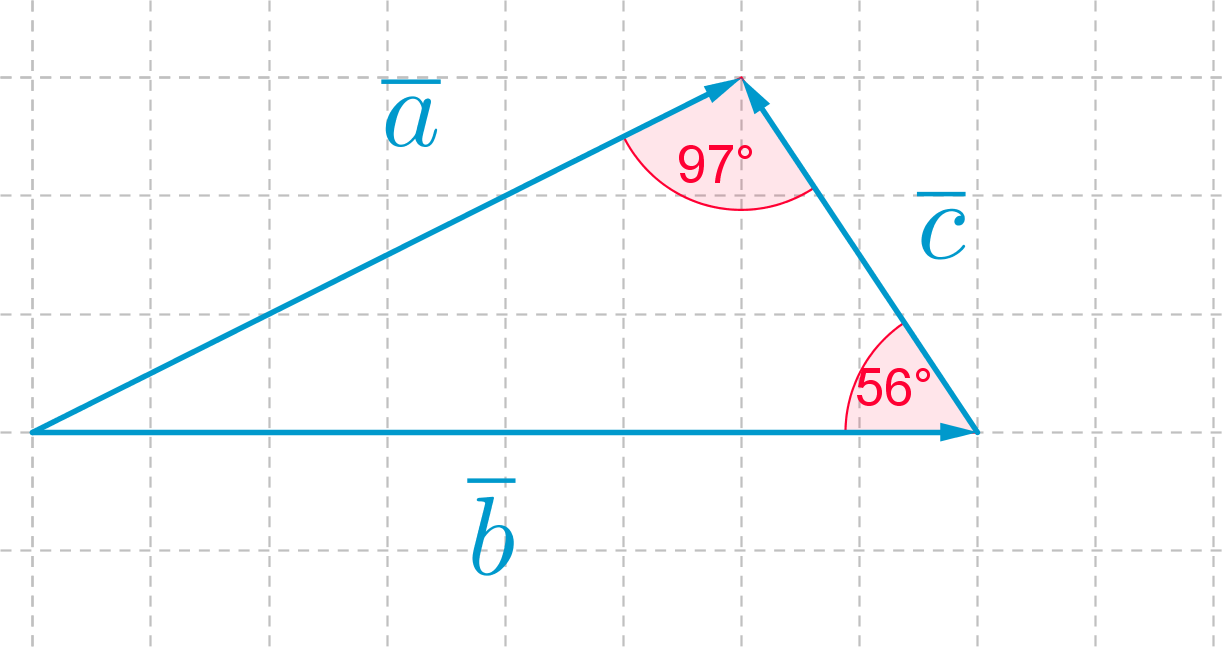
Vektorien välinen kulma on se kovera kulma, joka
muodostuu kun vektorit piirretään alkamaan samasta pisteestä
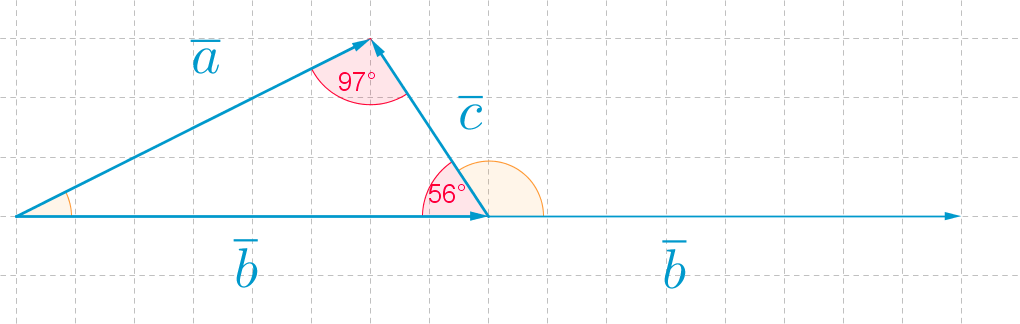
Vektorien \(\overline{a} \text{ ja } \overline{b}\) välinen kulma on
\(\angle(\overline{a}, \overline{b})=180^{\circ}-97^{\circ}-56^{\circ}\) \(\quad \color{red}{\text{(+1p)}}\)
\(\angle(\overline{a}, \overline{b})=27^{\circ}\) \(\quad \color{red}{\text{(+2p)}}\)
Vektorien \(\overline{b} \text{ ja } \overline{c}\) välinen kulma on
\(\angle(\overline{a}, \overline{b})=180^{\circ}-56^{\circ}\) \(\quad \color{red}{\text{(+1p)}}\)
\(\angle(\overline{a}, \overline{b})=124^{\circ}\) \(\quad \color{red}{\text{(+2p)}}\)
Ilmoita vektori \(\overline{c}\)vektorien \(\overline{a}\)ja \(\overline{b}\)avulla.
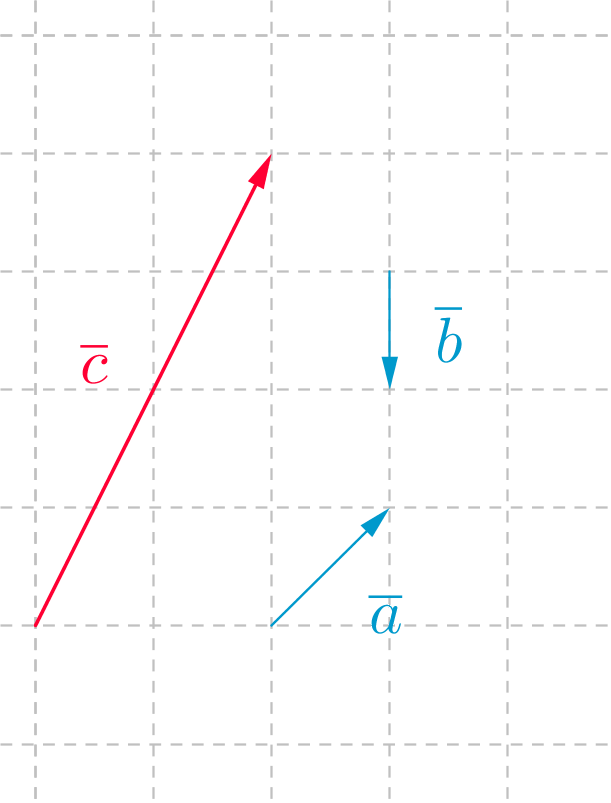
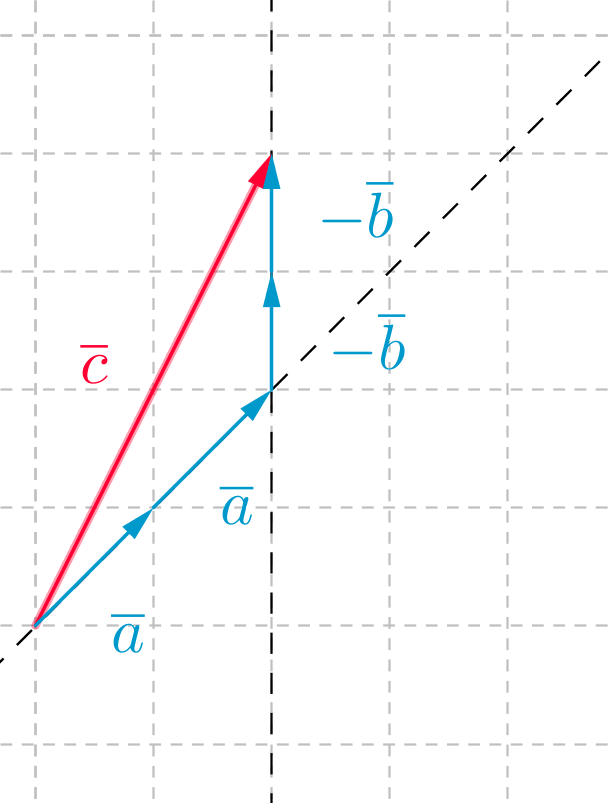
\(\quad \color{red}{\text{(Kuva oikein +3p)}}\)
Vektori \(\overline{c}\)voidaan ilmoittaa vektorien \(\overline{a} \text{ ja } \overline{ b}\)
avulla \(\overline{c}=2 \overline{a}-2\overline{b}\) \(\quad \color{red}{\text{(+3p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
