heittoliike
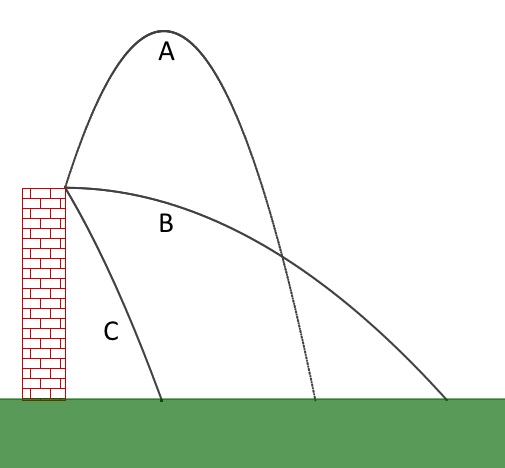
Pallo heitetään kolmella eri tavalla tornista.
Kaikissa tilanteissa pallon lähtönopeuden suuruus on sama.
Perustele missä tilanteessa pallo osuu suurimmalla vauhdilla maan pintaan?
a) Tilanteesssa A
b) Tilanteessa B
c) Tilanteessa C
d) Vauhti lopuksi on kaikissa tilanteissa sama
e) Tehtävää ei voi ratkaista annetuilla tiedoilla
Oletetaan, että palloon kohdistuva
ilmanvastus on mitätön.
Alussa pallon energia koostuu liike-energiasta ja potentiaalienergiasta.
Lähtökorkeus ja lähtönopeuden suuruus on kaikissa tilanteissa sama.
\(E_{aluksi}=mgh_0+\dfrac{1}{2}mv_0^2\) \(\color{red}{\text{(+1p)}}\)
Jokaisessa tilanteessa A, B ja C pallolla on
lähtötilanteessa yhtä paljon energiaa. \(\color{red}{\text{(+1p)}}\)
Energian säilymislain nojalla
\(E_{aluksi}=E_{lopuksi}\) \(\color{red}{\text{(+1p)}}\)
Asetetaan potentiaalienergian nollataso maanpinnalle.
Maanpintaan osuessaan pallolla
on vain liike-energiaa.
\(E_{lopuksi}=\dfrac{1}{2}mv_1^2\) \(\color{red}{\text{(+1p)}}\)
Jokaisessa tilanteessa pallon loppunopeuden
suuruus eli vauhti lopuksi on sama energian
säilymislain nojalla, joten oikea vastaus on d. \(\color{red}{\text{(+2p)}}\)
Tikka heitetään vaakasuoraan kohti maalitaulua.
Samanaikaisesti maalitaulu päästetään vapaasti putoamaan.
Tikka ja maalitaulu ovat lähtöhetkellä samalla korkeudella.
Minkä takia tikka osuu maalitauluun?
Hetkellä \(t=0,0 \text{ s}\) tikka heitetään vaakasuoraan
ja maalitaulu lähtee putoamaan korkeudelta \(y_0\).
Tarkastellaan tikan liikettä erikseen x- ja y-suunnassa.
Vaakasuunnassa tikan liike on tasaista.
\(x_t(t)=v_{0x}t\) \(\color{red}{\text{(+1p)}}\)
Pystysuunnassa tikan liike on tasaisesti kiihtyvää.
Tikan kiihtyvyys pystysuunnassa on \(g=9,81 \text{ m/s}^2\).
\(y_t(t)=y_0-\dfrac{1}{2}gt^2\) \(\color{red}{\text{(+1p)}}\)
Pystysuunnassa maalitaulun liike on tasaisesti kiihtyvää.
\(y_m(t)=y_0-\dfrac{1}{2}gt^2\) \(\color{red}{\text{(+1p)}}\)
Tikka ja maalitaulu etenevät pystysuunnassa saman matkan samassa ajassa, joten
molempien y-koordinaatti on jokaisella ajanhetkellä sama. \(\color{red}{\text{(+2p)}}\)
Jos tikka etenee vaakasuunnassa maalitaululle ajan, joka on lyhyempi kuin aika joka
kestää että maalitaulu putoaa lattiaan, niin tikka osuu maalitauluun. \(\color{red}{\text{(+1p)}}\)
Koripallo heitetään 2,0 metrin korkeudelta nopeudella 12 m/s.
Heittokulma muodostaa 30 asteen kulman maanpinnan kanssa.
a) Kuinka kauan kestää, että pallo nousee lakikorkeuteensa?
b) Kuinka kauan kestää, että pallo osuu maanpintaan?

a-kohdan ratkaisu
Kirjataan lähtöarvot
\(y_0=2,0 \text{ m}, \ v_0 = 12 \text{ m/s}\)
\(g=9,81 \text{ m/s}^2, \ \alpha=30^{\circ}\)
Piirretään kuva tilanteesta.
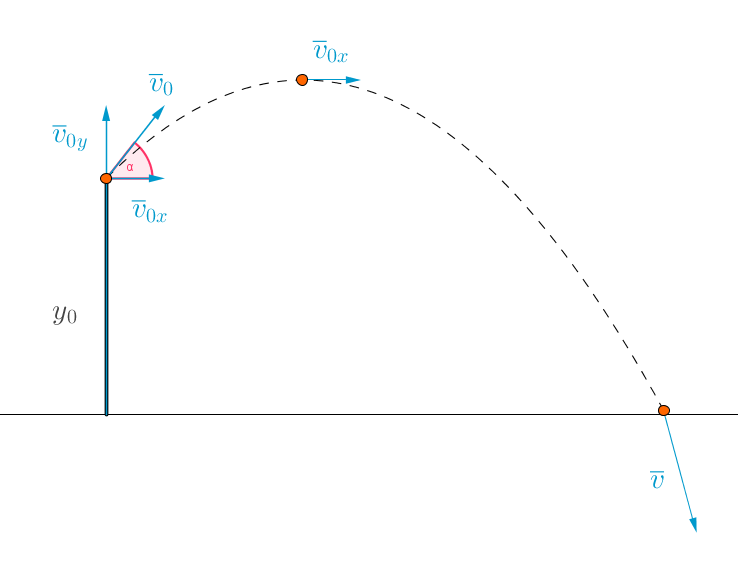
Oletetaan, että palloon kohdistuva ilmanvastus on mitätön. \(\color{red}{\text{(+0,5p)}}\)
Vaakasuunnassa koripallon liike on tasaista.
Pystysuunnassa koripallon liike on tasaisesti kiihtyvää.
Jaetaan nopeus x- ja y-suuntaisiin komponentteihin.
\(v_x=v_0 \cos \alpha\)
\(v_y=v_0 \sin \alpha - gt\)
Lakikorkeudella \(v_y=0\). \(\color{red}{\text{(+0,5p)}}\)
Ratkaistaan nousuaika \(t_n.\)
\(v_y= 0\)
\(v_0 \sin \alpha - gt_n = 0\)
\(t_n = \dfrac{v_0 \sin \alpha}{g}\) \(\color{red}{\text{(+0,5p)}}\)
\(t_n = \dfrac{12 \text{ m/s} \cdot \sin 30^{\circ}}{9,81 \text{ m/s}^2}\) \(\color{red}{\text{(+0,5p)}}\)
\(t_n \approx 0,612 \text{ s}\) \(\color{red}{\text{(+1p)}}\)
b-kohdan ratkaisu
Lasketaan lakikorkeus.
\(y_1=y_0 + v_0 \sin \alpha \cdot t_n- \dfrac{1}{2}gt_n^2\) \(\color{red}{\text{(+0,5p)}}\)
\(y_1=2,0 \text{ m} + 12 \text{ m/s} \cdot \sin 30^{\circ} \cdot 0,612 \text{ s} - \dfrac{1}{2}\cdot 9,81 \text{ m/s}^2 \cdot (0,612 \text{ s})^2\)
\(y_1 \approx 3,83 \text{ m}\) \(\color{red}{\text{(+0,5p)}}\)
Lasketaan kauanko kestää, että pallo putoaa lakikorkeudelta maanpintaan.
\(0=y_1 - \dfrac{1}{2}gt_p^2\) \(\color{red}{\text{(+0,5p)}}\)
\(\dfrac{1}{2}gt_p^2=y_1 \qquad ||\cdot 2\)
\(gt_p^2=2y_1 \qquad ||:g\)
\(t_p^2=\dfrac{2y_1}{g} \qquad ||\sqrt{}\)
\(t_p=\sqrt{\dfrac{2y_1}{g}} \) \(\color{red}{\text{(+0,5p)}}\)
\(t_p=\sqrt{\dfrac{2\cdot 3,83 \text{ m}}{9,81 \text{ m/s}^2}} \)
\(t_p \approx 0,884 \text{ s}\) \(\color{red}{\text{(+0,5p)}}\)
Pallon lentoaika on yhteensä
\(t_{kok}=t_n+t_p\)
\(t_{kok}= 0,612 \text{ s}+0,884 \text{ s}\)
\(t_{kok} \approx 1,5 \text{ s}\) \(\color{red}{\text{(+0,5p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
