Teoria
Vino heittoliike
Oletetaan, että palloon kohdistuva ilmanvastus on mitätön.
Jaetaan pallon liikkeen tarkastelu vaaka- ja pystysuuntaiseen tarkasteluun.
Vaakasuunnassa pallon liike on tasaista.
\(x(t)=v_{0x}t \\ v_x(t)=v_{0x}\)
Pystysuunnassa pallon liike on tasaisesti kiihtyvää.
\(y(t)=v_{0y}t-\dfrac{1}{2}gt^2 \\ v_y(t)=v_{0y}-gt\)
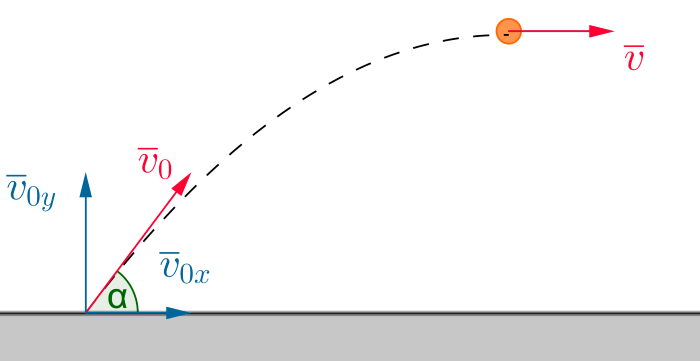
Alkunopeuden vaaka- ja pystysuuntaiset komponentit ovat
\(v_{0y}=v_0 \sin \alpha \\ v_{0x}=v_0 \cos \alpha\)
Lakikorkeudella pallon pystysuuntaisen nopeuden
suuruus on hetkellisesti nolla \(v_y=0 \text{ m/s}\).
Tämän avulla saadaan ratkaisua pallon nousuaika \(t_n\).
\(v_y=0 \\ v_{0y}-gt_n=0 \\ t_n = \dfrac{v_{0y}}{g}\)
Nopeus on vektorisuure, joten vastauksessa pitää
ilmoittaa nopeuden suuruus ja suunta.
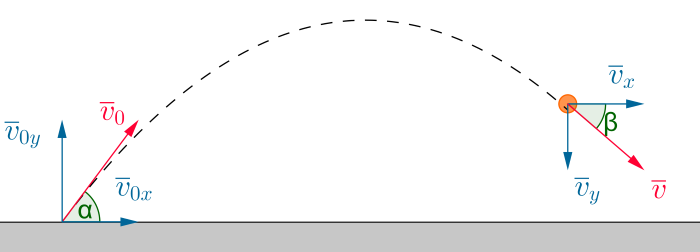
Nopeuden suuruus
\(v=\sqrt{v_x^2+v_y^2}\)
Nopeuden suunta
\(\tan \beta = \dfrac{v_y}{v_x}\)
Videot
Esimerkit
Kivi heitetään tornista vaakasuoraan nopeudella 20 m/s.
Kuinka korkea torni on, kun kivi lentää 100 metrin päähän tornista?
Kirjataan lähtöarvot
\(v_0=20 \text{ m/s}, \ \Delta x=100 \text{ m}\)
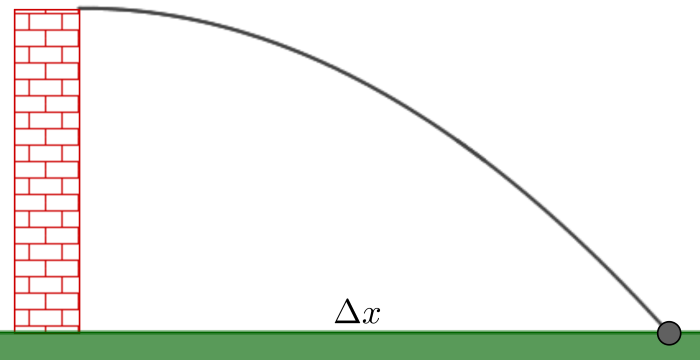
Oletetaan, että kiveen vaikuttava ilmanvastus on mitätön.
Vaakasuunnassa kiven liike on tasaista.
Ratkaistaan kiven lentoaika \(t\).
\(\Delta x = v_0 t\)
\(t=\dfrac{\Delta x}{v_0}\)
\(t=\dfrac{\Delta x}{v_0}\)
\(t=\dfrac{100 \text{ m}}{20 \text{ m/s}}\)
\(t=5,0 \text{ s}\)
Pystysuunnassa kivi on tasaisesti kiihtyvässä liikkeessä.
\(0 = y_0-\dfrac{1}{2}gt^2\)
\( y_0=\dfrac{1}{2}gt^2\)
\( y_0=\dfrac{1}{2} \cdot 9,81 \text{ m/s}^2 \cdot (5,0 \text{ s})^2\)
\( y_0 \approx 123 \text{ m}\)
Vastaus: Torni on noin 120 metriä korkea.
