Teoria
Ympyräliikkeessä kappaleen asento ja paikka muuttuvat.
Tasainen ympyräliike
Tasaisessa ympyräliikkeessä kappaleen ratanopeuden suuruus on vakio.
Ratanopeuden suuntaa muuttaa radan keskipistettä kohti suuntautuva normaalikiihtyvyys.
Normaalikiihtyvyyden ja ratanopeuden välinen suhde:
\(a_n = \dfrac{v^2}{r}\)
Jos kappale on tasaisessa ympyräliikkeessä, niin Newtonin 2. lain mukaan
\(\sum \overline{F}=m\overline{a}_n\)
Muuttuva ympyräliike
Muuttuvassa ympyräliikkeessä kappaleen ratanopeuden suuruus ja suunta muuttuvat.
Tangenttikiihtyvyys muuttaa ratanopeuden suuruutta.
\(a_t = \dfrac{\Delta v}{\Delta t}\)
Normaalikiihtyvyys muuttaa ratanopeuden suuntaa.
\(a_n = \dfrac{v^2}{r}\)
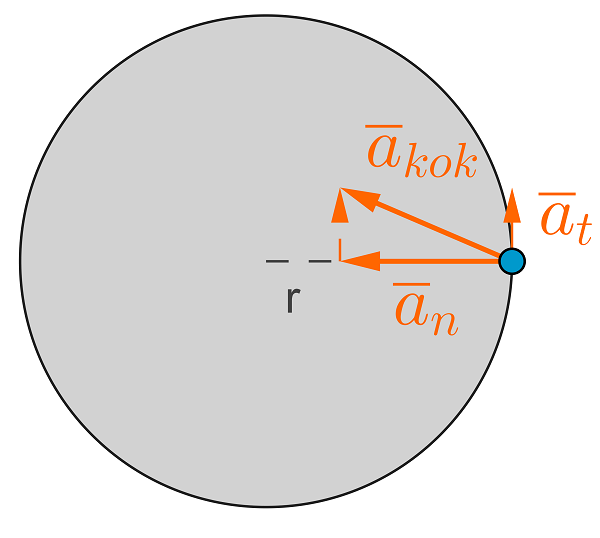
Kokonaiskiihtyvyyden ja kokonaisvoiman suuruudet
saadaan laskettua pythagoraan lauseen avulla.
\(a_{kok}=\sqrt{a_t^2+a_n^2} \\ F_{kok}=\sqrt{F_t^2+F_n^2}\)
Videot
Esimerkit
Esimerkki
Heiluri, jonka langan pituus on 50 cm, päästetään heilahtamaan 20 cm korkeudelta.
Heilurilanka on kevyt ja venymätön. Laske heilurin langan jännitysvoiman suuruus
hetkellä, jolloin punnus ohittaa alimman asemansa. Heilurin punnuksen massa on 0,200 kg.
Ratkaisu
Kirjataan lähtöarvot
\(r=0,50 \text{ m}, h=0,20 \text{ m}\)
\(g=9,81 \text{ m/s}^2\)
Piirretään kuva tilanteesta.
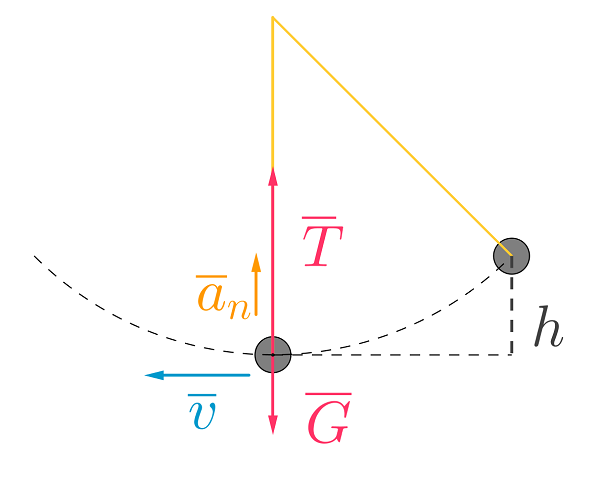
Tarkastellaan heiluriin vaikuttavia voimia heilurin radan alimmassa kohdassa.
Newtonin 2. lain mukaan
\(\sum \overline{F}=m\overline{a}\)
Oletetaan, että heiluri on tasaisessa ympyräliikkeessä radan alimmassa kohdassa.
\(\overline{G}+\overline{T}=m\overline{a}_n\)
Sovitaan suunnat ylös ja vasemmalle positiivisiksi.
\(-G+T=m\dfrac{v^2}{r}\)
\(T=m\dfrac{v^2}{r}+mg\)
Ratkaistaan heilurin ratanopeuden \(v\) suuruus.
Oletetaan, että mekaaninen energia säilyy.
Valitaan potentiaalienergian nollakohdaksi heilurin radan alin kohta.
\(E_{aluksi}=E_{lopuksi}\)
\(mgh = \dfrac{1}{2}mv^2\)
\(2gh=v^2\)
\(v=\sqrt{2gh}\)
Sijoitetaan lukuarvot
\(v=\sqrt{2 \cdot 9,81 \text{ m/s}^2 \cdot 0,20 \text{ m}}\)
\(v \approx 1,98 \text{ m/s}\)
Lasketaan heilurin langan jännitysvoiman suuruus
\(T=m\dfrac{v^2}{r}+mg\)
\(T=0,200 \text{ kg} \cdot \dfrac{(1,98 \text{ m/s})^2}{0,50 \text{ m}}+0,200 \text{ kg} \cdot 9,81 \text{ m/s}^2\)
\(T \approx 3,5 \text{ N}\)
Vastaus: Heilurin langan jännitysvoiman suuruus on noin 3,5 N.
