tasainen ja muuttuva ympyräliike
Oheisen kiertoheilurin langan jännitysvoima on punnuksen painoon verrattuna
a) suurempi
b) pienempi
c) yhtä suuri
d) välillä suurempi ja välillä pienempi
Perustele vastauksesi.
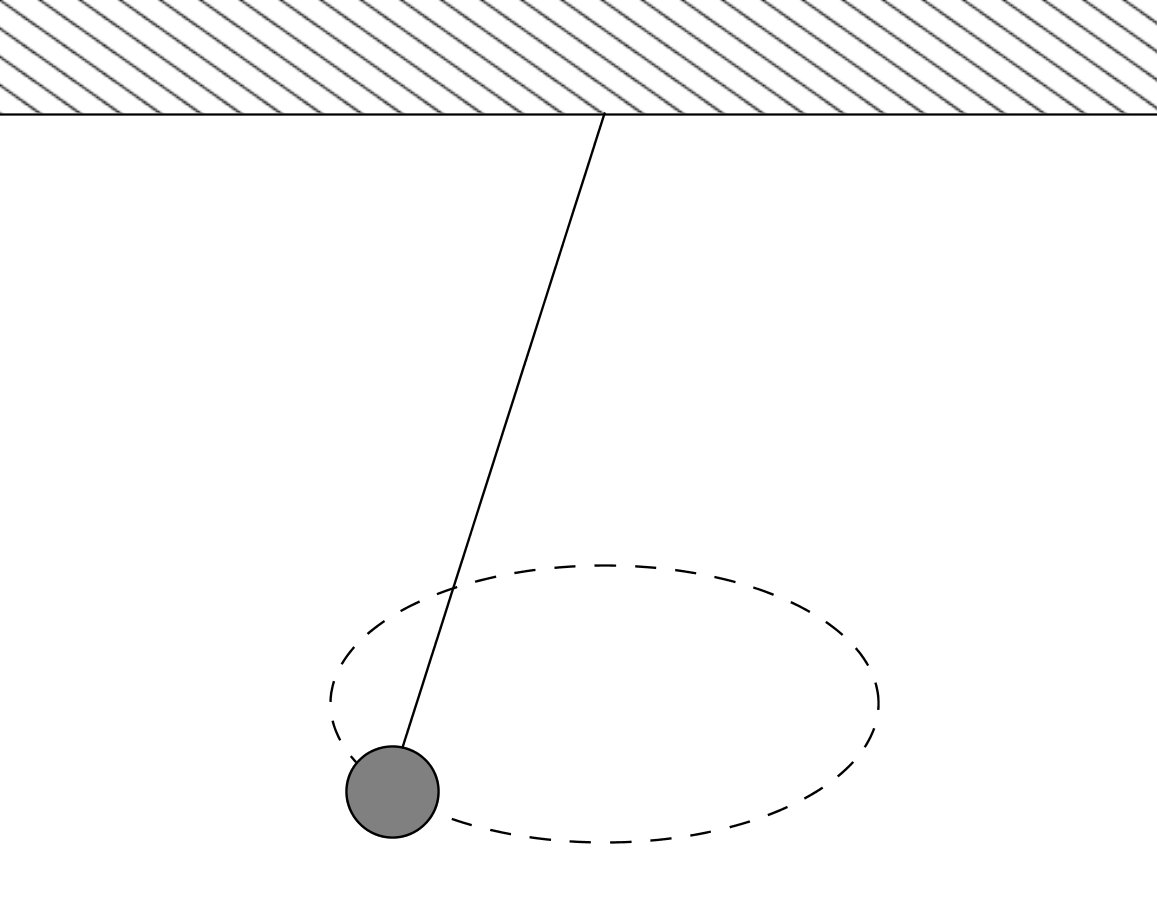
Piirretään heilurin voimakuvio.
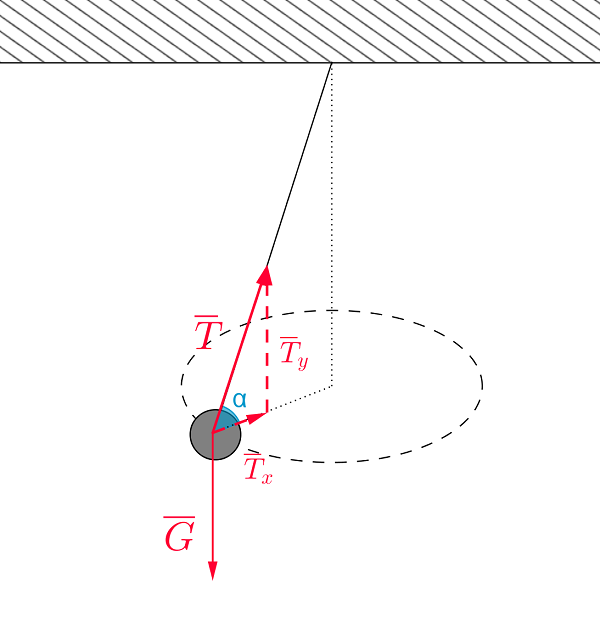
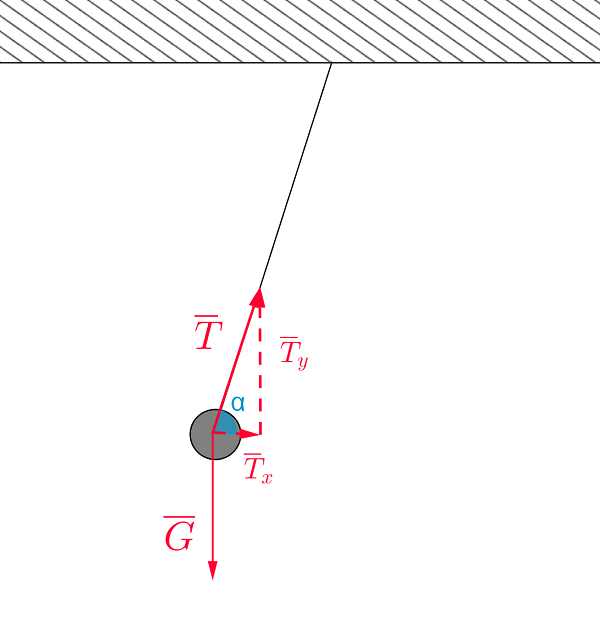
\(\color{red}{\text{(voimakuvio oikein +1p)}}\)
Oletetaan, että kiertoheiluri on tasaisessa ympyräliikkeessä.
Tällöin heilurilla on kiihtyvyyttä ainoastaan kohti ympyräradan keskipistettä.
Newtonin 2. lain eli dynamiikan peruslain mukaan \(\color{red}{\text{(+1p)}}\)
\(\sum \overline{F}=m\overline{a}_n\)
\(\overline{G}+\overline{T}=m\overline{a}_n\)
Jaetaan voimatarkastelu x- ja y-suuntiin.
\(\sum \overline{F}_x=m\overline{a}_n\)
\(\overline{T}_x=m\overline{a}_n\)
\(T \cos \alpha=ma_n\)
\(\sum \overline{F}_y=\overline{0}\)
\(\overline{G}+\overline{T}_y=\overline{0}\)
\(-G+T_y=0\)
\(T \sin \alpha = G\) \(\color{red}{\text{(+1p)}}\)
\(T = \dfrac{G}{\sin \alpha} \geq G \qquad || 0^{\circ} \leq \alpha \leq 90^{\circ}\) \(\color{red}{\text{(+1p)}}\)
Sinin arvo on suurimmillaan 1, joten pätee:
\(T \geq G\) \(\color{red}{\text{(+1p)}}\)
Vastaus: langan jännitysvoima on suurempi kuin
heilurin paino eli a-kohta on oikein. \(\color{red}{\text{(+1p)}}\)
Moukarinheittäjä pyörittää moukaria. Moukarin pituus on 120 cm.
Eräällä hetkellä moukarin tangenttikiihtyvyyden suuruus \(1,1 \text{ m/s}^2\)
ja moukarin ratanopeus on \(1,5 \text{ m/s}\).
Kuinka suuri on moukarin kiihtyvyys?

Kirjataan lähtöarvot
\(r=1,2 \text{ m}, a_t=1,1 \text{ m/s}^2, \ v=1,5 \text{ m/s}\)
Piirretään kuva tilanteesta
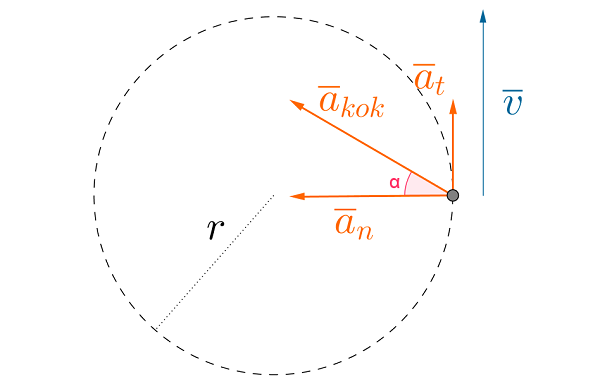
\(\color{red}{\text{(Kuva oikein +1p)}}\)
Normaalikiihtyvyyden ja ratanopeuden välinen yhteys:
\(a_n = \dfrac{v^2}{r}\)
\(a_n = \dfrac{(1,5 \text{ m/s})^2}{1,2 \text{ m}}\)
\(a_n = 1,875 \text{ m/s}^2\) \(\color{red}{\text{(+1p)}}\)
Moukarin kokonaiskiihtyvyyden suuruus saadaan
pythagoraan lauseen avulla
\(a_{kok}=\sqrt{a_n^2+a_t^2}\) \(\color{red}{\text{(+1p)}}\)
\(a_{kok}=\sqrt{(1,875 \text{ m/s}^2)^2+(1,1 \text{ m/s}^2)^2}\)
\(a_{kok}=\sqrt{(1,875 \text{ m/s}^2)^2+(1,1 \text{ m/s}^2)^2}\)
\(a_{kok} \approx 2,2 \text{ m/s}^2\) \(\color{red}{\text{(+1p)}}\)
Kokonaiskiihtyvyyden suunta saadaan ratkaistua tangentin avulla
\(\tan \alpha =\dfrac{a_t}{a_n}\)
\(\tan \alpha =\dfrac{1,1 \text{ m/s}^2}{1,875 \text{ m/s}^2} \qquad ||\tan^{-1}\)
\(\alpha \approx 30^{\circ}\) \(\color{red}{\text{(+1p)}}\)
Vastaus: Kiihtyvyyden suuruus on noin 2,2 \(\text{ m/s}^2\)
ja suunta poikkeaa 30 astetta normaalikiihtyvyyden suunnasta. \(\color{red}{\text{(+1p)}}\)
Kolme tulitikkurasiaa asetetaan kuvan mukaisesti pyörivälle alustalle.
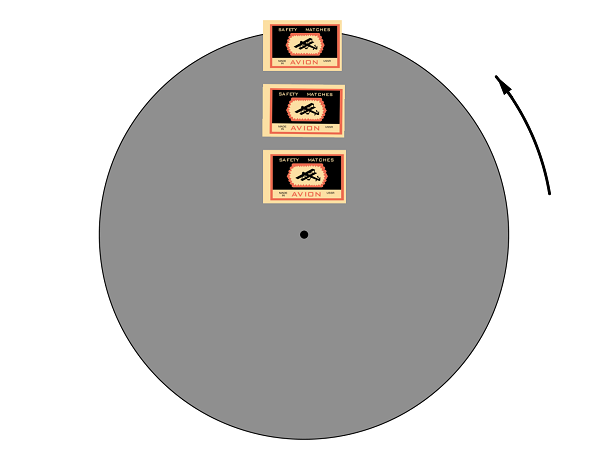
Alusta pyöräytetään liikkeelle.
Mikä tulitikkurasioista irtoaa ensimmäisenä? Miksi?
Kun alusta pyöräytetään liikkeelle, niin tulitikkurasiat
ovat kiihtyvässä liikkeessä.
Newtonin 2. lain mukaan
\(\sum \overline{F}=m\overline{a}\)
\(\overline{G}+\overline{N}+\overline{F}_\mu=m\overline{a}\) \(\color{red}{\text{(+1p)}}\)
Paino ja pinnan tukivoima ovat yhtä suuret ja vastakkaissuuntaiset,
joten kitka pitää tulitikkurasiat ympyräradalla.
\(F_\mu = m a\) \(\color{red}{\text{(+1p)}}\)
Tulitikkurasian kiihtyvyys saadaan tangentti- ja normaalikiihtyvyyden vektorisummana
\(\overline{a}=\overline{a}_t+\overline{a}_n\).
Tulitikkurasian kiihtyvyyden suuruus saadaan pythagoraan lauseen avulla
\(a=\sqrt{a_t^2+a_n^2}\) \(\color{red}{\text{(+1p)}}\)
\(a=\sqrt{\Big(\dfrac{\Delta v}{\Delta t}\Big)^2+\Big(\dfrac{v^2}{r}\Big)^2}\).
Kun alustan pyörimisnopeus kasvaa, niin kasvaa myös tulitikkurasian ratanopeus.
Ensimmäisenä irtoaa se tulitikkurasia, joka on kauimpana pyörimisakselista. \(\color{red}{\text{(+2p)}}\)
Tämä johtuu siitä, että sen paikalla pitämiseen tarvittava kitkavoima on kaikista suurin. \(\color{red}{\text{(+2p)}}\)
HUOM!
\(a_t = \alpha r\)
\(v=\omega r\)
Kulmakiihtyvyys \(\alpha \) ja kulmanopeus \(\omega\)
ovat jokaisella tulitikkurasialla samat.
\(a=\sqrt{a_t^2+a_n^2}\)
\(a=\sqrt{(\alpha r)^2+(\omega r)^2}\)
\(a=\sqrt{r^2(\alpha^2+\omega^2)}\)
\(a=r\underbrace{\sqrt{(\alpha^2+\omega^2)}}_{\text{kaikilla sama}}\)
Tarvittavan kitkavoiman suuruus saadaan siis kirjoitettua muotoon
\(F_\mu = m a\)
\(F_\mu = mr\underbrace{\sqrt{(\alpha^2+\omega^2)}}_{\text{kaikilla sama}}\)
\(F_\mu = r\underbrace{m\sqrt{(\alpha^2+\omega^2)}}_{\text{kaikilla sama}}\)
Mitä kaueampana tulitikkurasia on pyörimisakselista, niin sitä suurempi on tarvittavan kitkavoiman suuruus.
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
