Gravitaatio ja gravitaation aiheuttama ympyräliike
Putoava omena ja Maapallo vetävät toisiaan puoleensa yhtä suurilla mutta
vastakkaissuuntaisilla voimilla Newtonin 3. lain mukaan.
a) Miksi omena liikkuu mutta Maapallo ei?
b) Kuinka suuri on omenan aiheuttama kiihtyvyys Maapallolle, jos omenan massa on 100 g?
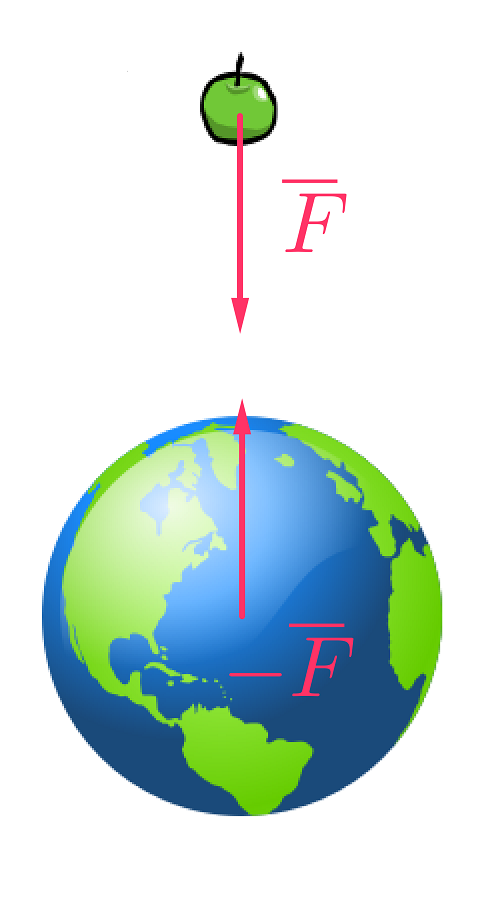
a) Molempiin kappaleisiin vaikuttaa Newtonin 3. lain mukaan yhtä suuret, mutta vastakkaissuuntaiset voimat.
Newtonin 2. lain mukaan \(F=ma\), josta \(a=\dfrac{F}{m}\). \(\color{red}{\text{(+2p)}}\)
Omenan saaman kiihtyvyyden suuruus on
\(a_{omena}=\dfrac{F}{m_{omena}}\)
Maapallon saaman kiihtyvyyden suuruus on
\(a_{maa}=\dfrac{-F}{M_{maa}}\)

b) Oletetaan, että omena on lähellä Maapallon pintaa.
Jos omenan massa on 100 g, niin omenaan kohdistuvan painon suuruus on
\(G=mg \\ G=0,100 \text{ kg} \cdot (-9,81 \text{ m/s}^2) \\ G=-0,981 \text{ N}\)
\(\color{red}{\text{(Paino oikein +1p)}}\)
Toisaalta Maapalloon kohdistuu yhtä suuri, mutta vastakkaissuuntainen voima -G Newtonin 3. lain mukaan. \(\color{red}{\text{(+1p)}}\)
Newtonin 2. lain avulla saadaan laskettua maapallon kiihtyvyys.
\(G=ma \\ a=\dfrac{-G}{m} \\ a= \dfrac{-(-0,981 \text{ N})}{5,974 \cdot 10^{24} \text{ kg}} \\ a\approx 1,6 \cdot 10^{-25} \text{ m/s}^2\)
Vastaus: Maapallon kiihtyvyys on noin \(1,6 \cdot 10^{-25} \text{ m/s}^2\) \(\color{red}{\text{(+1p)}}\)
Laika niminen koira lähetettiin Maata kiertävälle radalle Neuvostoliittolaisessa Sputnik 2 -satelliitissa vuonna 1957.
Sekarotuinen Laika oli yksi ensimmäisistä elävistä olennoista Maapallon kiertoradalla. Laikan massa oli noin 6,5 kg.

Kuinka suuri oli Laika -koiraan kohdistuvan painon suuruus, kun Sputnik 2 -satelliitti oli
a) 210 km korkeudella Maapallon pinnasta?
b) 1700 km korkeudella Maapallon pinnasta?
Kirjataan lähtöarvot.
\(r_1=6370 \text{ km}+210 \text{ km}=6580 \text{ km} \\ r_2=6370 \text{ km} + 1700 \text{ km} = 8070 \text{ km} \\ \gamma = 6,6742 \cdot 10^{-11} \frac{\text{Nm}^2}{\text{kg}^2} \\ M=5,974 \cdot 10^{24} \text{ kg} \\ m=6,5 \text{ kg}\)
Sovelletaan Newtonin gravitaatiolakia.
\(F=\gamma \dfrac{mM}{r^2}\) \(\color{red}{\text{(+1p)}}\)
\(F_1=6,6742 \cdot 10^{-11} \frac{\text{Nm}^2}{\text{kg}^2} \dfrac{6,5 \text{ kg} \cdot 5,974 \cdot 10^{24 } \text{ kg}}{(6 \ 580 \ 000 \text{ m})^2}\) \(\color{red}{\text{(+1p)}}\)
\(F_1 \approx 60 \text{ N}\) \(\color{red}{\text{(+1p)}}\)
\(F_1=6,6742 \cdot 10^{-11} \frac{\text{Nm}^2}{\text{kg}^2} \dfrac{6,5 \text{ kg} \cdot 5,974 \cdot 10^{24 } \text{ kg}}{(8 \ 070 \ 000 \text{ m})^2}\) \(\color{red}{\text{(+1p)}}\)
\(F_2 \approx 40 \text{ N}\) \(\color{red}{\text{(+1p)}}\)
Vastaus: Laikan paino 210 km korkeudella on noin 60 N ja
paino 1700 km korkeudella on noin 40 N. \(\color{red}{\text{(+1p)}}\)
Satelliitti kiertää Maapalloa 35 000 km korkeudella.
a) Laske satelliitin nopeuden suuruus
b) Laske satelliitin kiertoaika

a) Kirjataan lähtöarvot
\(r=6370 \text{ km} + 35 \ 000 \text{ km} = 41 \ 370 \text{ km}\)
\(M=5,974 \cdot 10^{24} \text{ kg} \\ \gamma = 6,6742 \cdot 10^{-11} \frac{\text{Nm}^2}{\text{kg}^2}\)
Piirretään kuva tilanteesta.
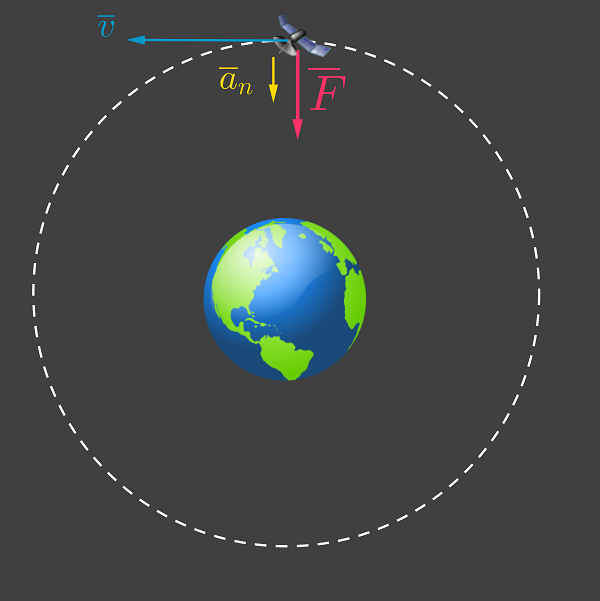
Oletetaan, että satelliitti on tasaisessa ympyräliikkeessä Maapallon ympäri. \(\color{red}{\text{(+1p)}}\)
Gravitaatiovoima aiheuttaa satelliitin normaalikiihtyvyyden kohti ympyräradan keskipistettä.
Newtonin 2. lain mukaan satelliitin liikeyhtälö saa muodon:
\(\begin{align*} \sum \overline{F}&=m\overline{a} \\ F&=ma_n \\ \gamma \dfrac{mM}{r^2}&=m\dfrac{v^2}{r} \qquad &&||:m \\ \gamma \dfrac{M}{r^2}&=\dfrac{v^2}{r} \qquad &&|| \cdot r \\ \gamma \dfrac{M}{r}&=v^2 \qquad &&||\sqrt{} \\ v&= \sqrt{\dfrac{\gamma M}{r}} \end{align*}\)
\(\color{red}{\text{( +1p)}}\)
Sijoittaan tunnetut lukuarvot ja ratkaistaan satelliitin ratanopeus.
\(\begin{align*} v&= \sqrt{\dfrac{\gamma M}{r}} \\ v&=\sqrt{\dfrac{6,6742 \cdot 10^{-11} \frac{\text{Nm}^2 }{\text{kg}^2} \cdot 5,974 \cdot 10^{24} \text{ kg} }{41 \ 370 \ 000 \text{ m}}} \end{align*}\)
\(v \approx 3,1 \text{ km/s}\)
Vastaus: Satelliitin ratanopeus on noin 3,1 km/s. \(\color{red}{\text{(+1p)}}\)
b) Satelliitin kiertoaika saadaan laskettua, kun tiedetään ympyräradan pituus ja ratanopeus.
\(T=\dfrac{2 \pi r}{v}\) \(\color{red}{\text{(+1p)}}\)
\(T=\dfrac{2 \pi\cdot 41 \ 370 \ 000 \text{ m} }{3104 \text{ m/s}} \) \(\color{red}{\text{(+1p)}}\)
\(T \approx 83 \ 742 \text{ s} \\ T \approx 23 \text{ h} \ 16 \text{ min}\)
Vastaus: Satelliitin kiertoaika on noin 23 h 16 min \(\color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
