Tutki oheisen sovelluksen avulla, milloin lauta on tasapainossa pyörimisen suhteen.
Muotoile laudan tasapainoehto etenemisen ja pyörimisen suhteen.
Newtonin 2. lain mukaan lauta on tasapainossa etenemisen suhteen, kun
\(\sum \overline{F}=\overline{0}\) \(\color{red}{\text{(+1p)}}\)
\(\overline{N}+\overline{G}_1+\overline{G}_2=\overline{0}\) \(\color{red}{\text{(+1p)}}\)
\(N-G_1-G_2=0\) \(\color{red}{\text{(+1p)}}\)
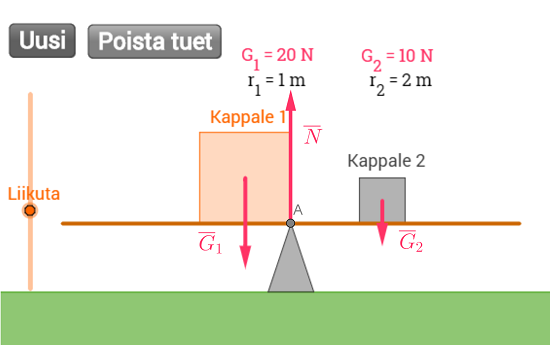
Lauta on tasapainossa pyörimisen suhteen, kun
\(\sum M=0\).
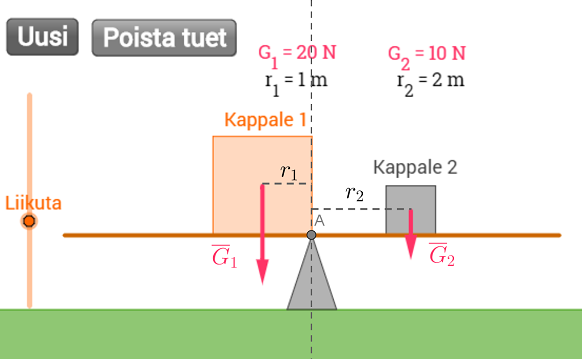
Valitaan pyörimisakseliksi piste A.
Lauta on tasapainossa pyörimisen suhteen, kun
\(\begin{align*} \sum M_A&=0 \qquad &&\color{Red}{\text{(+1p)}}\\ G_1 r_1 - G_2 r_2& = 0 &&\color{Red}{\text{(+1p)}} \\ G_1 r_1& = G_2 r_2 &&\color{Red}{\text{(+1p)}}\end{align*}\)
(Huom! \(\overline{N}\)ei aiheuta momenttia akselin A suhteen)
Isä ja poika kantavat rakennustyömaalla 6,4 m:n pituista tasapaksua hirttä, jonka massa on 150 kg. Poika kykenee kannattelemaan 560 N:n kuormaa.
a) Kuinka suuri voima vähintään kohdistuu isän käsiin, kun he pitävät hirttä käsiensä varassa vaakasuorassa asennossa?
b) Mikä on tällöin isän ja pojan otteen paikka, kun toinen heistä kannattelee hirttä sen päästä?
(Fysiikan ylioppilaskoe, kevät 2001, tehtävä 6)
Kirjataan lähtöarvot
\(l=6,4 \text{ m}, \ m=150 \text{ kg}, \ N_1 = 560 \text{ N}\)
Piirretään kuva tilanteesta.
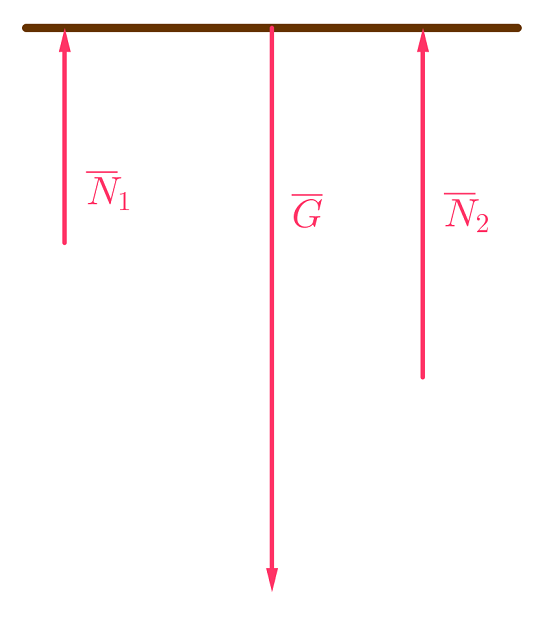
a) Hirsi on tasapainossa etenemisen suhteen, joten Newtonin 2. lain eli dynamiikan peruslain mukaan \(\color{Red}{\text{(+0,5p)}}\)
\(\sum \overline{F}=\overline{0}\)
\(\overline{G}+\overline{N}_1+\overline{N}_2=\overline{0}\)
\(-G+N_1+N_2=0\)
\(N_2 = G - N_1\) \(\color{Red}{\text{(+0,5p)}}\)
\(N_2 = 150 \text{ kg} \cdot 9,81 \text{ m/s}^2 - 560 \text{ N}\) \(\color{Red}{\text{(+1p)}}\)
\(N_2 = 911,5 \text{ N}\)
Isän kädet kohdistavat tukkiin noin 910 N suuruisen voiman, jolloin
tukki kohdistaa isän käsiin Newtonin 3. lain mukaan yhtä suuren, mutta vastakkaissuuntaisen voiman.
Vastaus: Isän käsiin kohdistuu vähintään 910 N suuruinen voima. \(\color{Red}{\text{(+1p)}}\)
b) Isä tai poika kannattelee hirttä sen päästä, joten isän tai pojan kohdistaman tukivoiman momentti
akselin A suhteen on nolla.
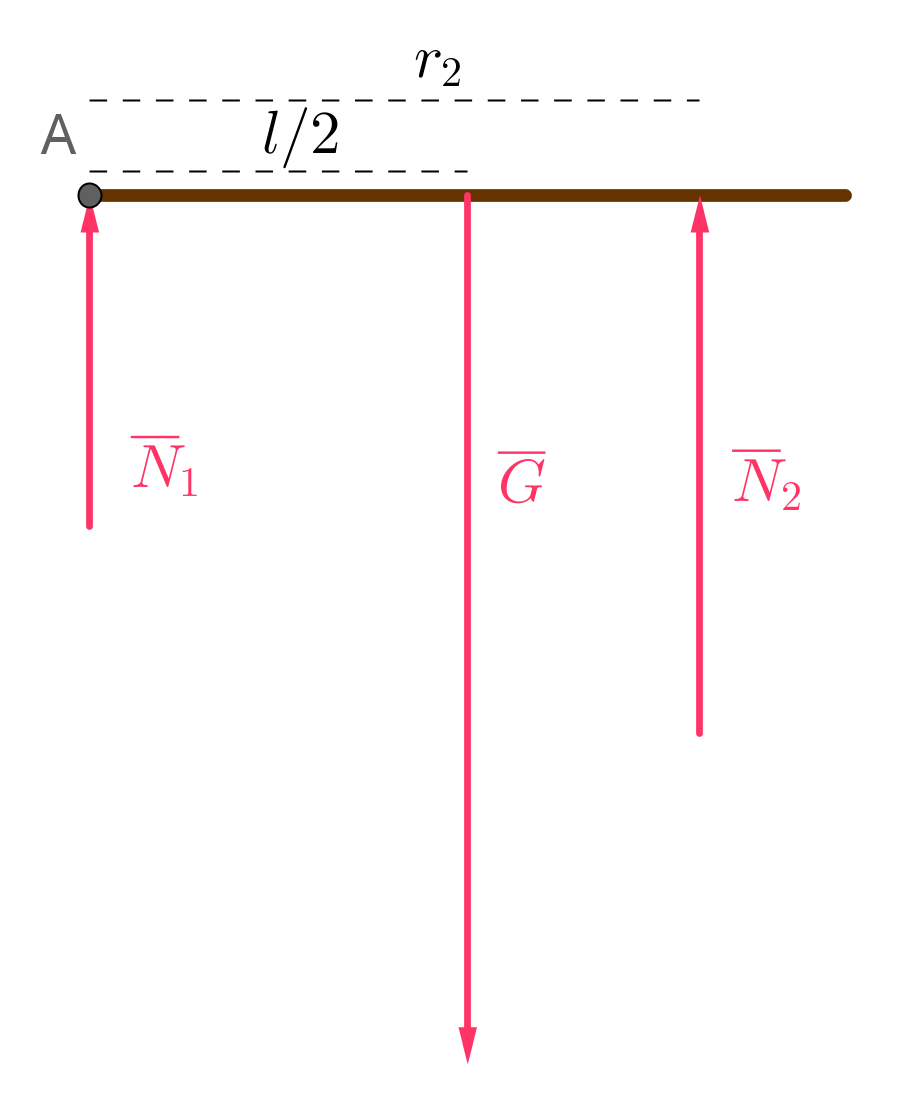
Isän paikka, jos poika kannattelee hirttä pisteessä A.
\(\sum M = 0\) \(\color{Red}{\text{(+0,5p)}}\)
\(N_2 r_2 - G \dfrac{l}{2}=0\) \(\color{Red}{\text{(+1p)}}\)
\(N_2 r_2= G \dfrac{l}{2}\)
\(r_2 = \dfrac{Gl}{2 N_2}\)
\(r_2 = \dfrac{150 \text{ kg} \cdot 9,81 \text{ m/s}^2 \cdot 6,4 \text{ m}}{2 \cdot 911,5 \text{ N}}\) \(\color{Red}{\text{(+0,5p)}}\)
\(r_2 \approx 5,2 \text{ m}\) \(\color{Red}{\text{(+1p)}}\)
\(6,4 \text{ m} - 5,2 \text{ m} = 1,2 \text{ m}\)
\(\sum M = 0\)
\(N_1 r_1 - G \dfrac{l}{2}=0\)
\(N_1 r_1= G \dfrac{l}{2}\)
\(r_1 = \dfrac{Gl}{2 N_1}\)
\(r_1 = \dfrac{150 \text{ kg} \cdot 9,81 \text{ m/s}^2 \cdot 6,4 \text{ m}}{2 \cdot 560 \text{ N}}\) \(\color{Red}{\text{(+0,5p)}}\)
\(r_1 \approx 8,4 \text{ m}\) \(\color{Red}{\text{(+0,5p)}}\)
Poika ei jaksaisi kannatella hirttä, jos isä kannattelisi hirttä sen päästä.\(\color{Red}{\text{(+1p)}}\)
Vastaus: Poika kannattelee hirren päästä ja isä 5,6 metrin etäisyydellä pojasta. \(\color{Red}{\text{(+1p)}}\)
Partiolainen lämmittelee hernekeittopurkkia, jonka massa on 500g, kuvan osoittamalla tavalla.
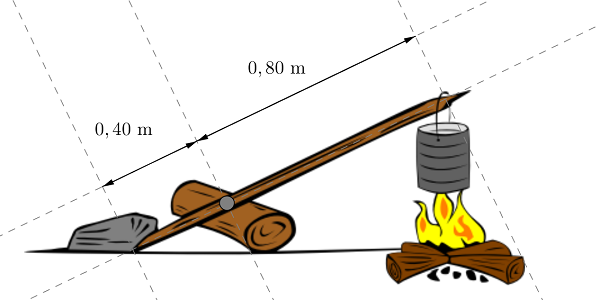
Mikä on kiven massan vähintään oltava, jos keppi muodostaa 30 asteen kulman maanpinnan kanssa?
Kepin massa on 1,2 kg.
Kirjataan lähtöarvot
\(m_2 = 1,2 \text{ kg}\)
\(m_3 = 0,500 \text{ kg}\)
\(r_3 = 0,80 \text{ m}\)
\(r_1 = 0,40 \text{ m}\)
Piirretään kuva tilanteesta
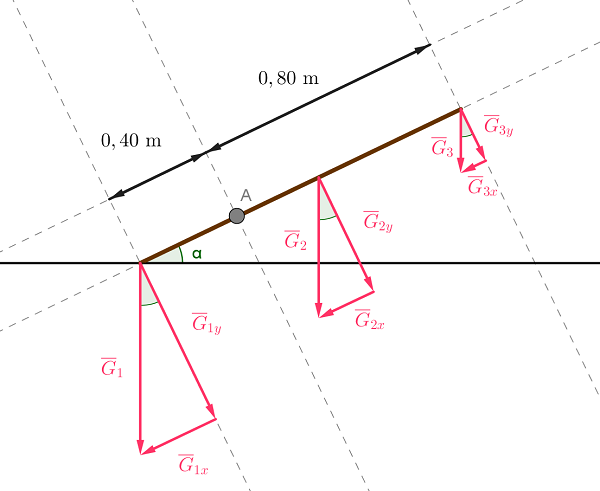
Rajatilanteessa, jossa keppi juuri ja juuri pysyy tasapainossa maanpinnan kohdistama
tukivoima keppiin on likimain nolla \((N_1 \approx 0 \text{ N})\). \(\color{Red}{\text{(+1p)}}\)
Tukin kohdistama tukivoima keppiin ei aiheuta momenttia, koska se kohdistuu
suoraan kiertoakseliin A.
Oletetaan, että keppi on tasapaksu ja homogeeninen kauttaaltaan.
Tällöin kepin painopiste sijaitsee puolessa välissä keppiä.
Painopisteen etäisyys kiertoakselista A on
\(r_2 = 0,20 \text{ m}\). \(\color{Red}{\text{(+1p)}}\)
Oletetaan, että keppi on tasapainossa pyörimisen suhteen ja valitaan pyörimisakseliksi piste A.
\(\sum M_A = 0\) \(\color{Red}{\text{(+1p)}}\)
\(G_{1y}r_1 - G_{2y}r_2-G_{3y}r_3=0\) \(\color{Red}{\text{(+1p)}}\)
\(G_{1y}r_1 = G_{2y}r_2+G_{3y}r_3=0\)
\(G_{1}r_1\cos \alpha = G_{2}r_2 \cos \alpha+G_{3}r_3\cos \alpha\)
\(G_{1}r_1 = G_{2}r_2 +G_{3}r_3\)
\(m_1 gr_1 = m_2 gr_2 + m_3 gr_3\)
\(m_1 r_1 = m_2 r_2 + m_3 r_3\)
\(m_1 = \dfrac{m_2 r_2 + m_3 r_3}{r_1}\) \(\color{Red}{\text{(+1p)}}\)
Sijoitetaan tunnetut lukuarvot.
\(m_1 = \dfrac{1,2 \text{ kg} \cdot 0,20 \text{ m} + 0,500 \text{ kg} \cdot 0,80 \text{ m}}{0,40 \text{ m}}\)
\(m_1 = 1,6 \text{ kg}\)
Vastaus: Kiven massan tulee olla vähintään 1,6 kg. \(\color{Red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
