Teoria
Momentti
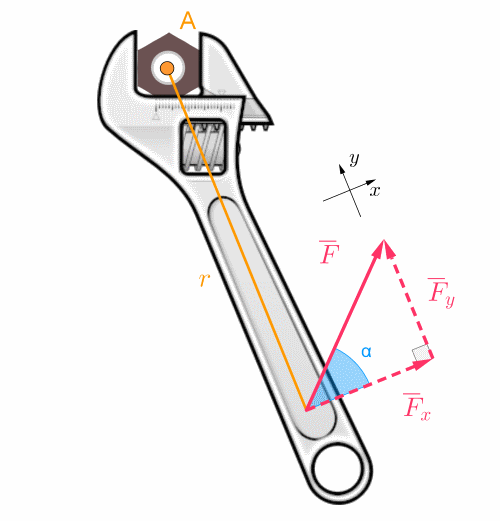
Voiman F momentti pyörimisakselin A suhteen on
\(\begin{align} M_A&=F_x \cdot r \\ M_A&=F r\cos \alpha \end{align}\)
Etenemisen tasapaino
Kappale on tasapainossa etenemiseen suhteen jos
kappaleeseen vaikuttava kokonaisvoima on nolla.
\(\sum \overline{F}=\overline{0}\)
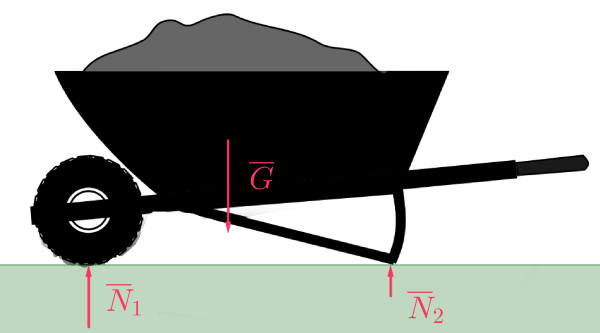
\(\begin{align} \sum \overline{F}&=\overline{0} \\ \overline{G}+\overline{N}_1+\overline{N}_2&=\overline{0}\\ -G+N_1+N_2&=0 \\ N_1+N_2&=G \end{align}\)
Pyörimisen tasapaino
Kappale on tasapainossa pyörimisen suhteen jos
kappaleeseen vaikuttava kokonaismomentti on nolla.
\(\sum M=0\)
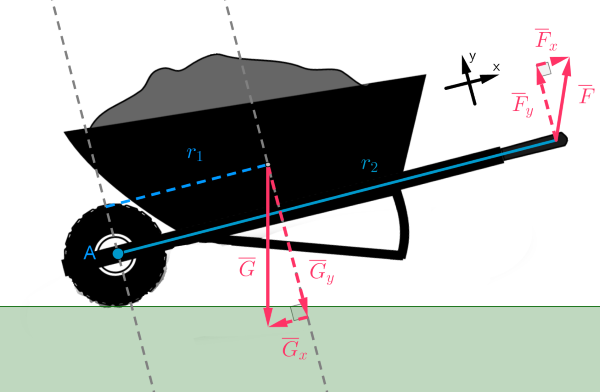
Jos kottikärry on tasapainossa pyörimisen suhteen, niin
\(\begin{align} \sum M_A&=0 \\ -G_y \cdot r_1 + F_y \cdot r_2&=0 \\ F_y \cdot r_2 &= G_y \cdot r_1 \end{align}\)
