Teoria
Pyörimisliikkeessä kappaleen asento muuttuu.
Tasainen pyörimisliike
Kiertokulma \(\varphi\)
Kiertymä \(\Delta \varphi\)
Kulmanopeus \(\omega = \dfrac{\Delta \varphi}{\Delta t}\)
\([\omega]=1 \text{ rad/s}\)
Tasaisessa pyörimisliikkeessä kappaleen kulmanopeus on vakio.
Tasaisesti muuttuva pyörimisliike
Kulmakiihtyvyys \(\alpha = \dfrac{\Delta \omega}{\Delta t}\)
\([\alpha]=1 \text{ rad/s}^2\)
Tasaisesti muuttuvassa pyörimisliikkeessä kappaleen kulmakiihtyvyys on vakio.
Kulmanopeuden ja ratanopeus
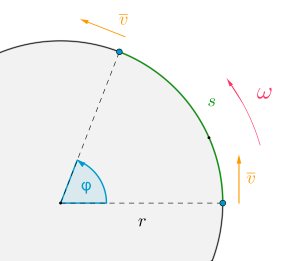
Kulma radiaaneina määritellään ympyräkaaren pituuden ja ympyrän säteen suhteena
\(\varphi = \dfrac{s}{r}\) eli \(s=\varphi r\)
Ratkaistaan ratanopeuden ja kulmanopeuden välinen suhde.
\(\begin{align} v&=\dfrac{s}{\Delta t} \\ v&=\dfrac{\Delta \varphi\cdot r}{\Delta t}\\ v&=\dfrac{\Delta \varphi}{\Delta t} \cdot r \\ v&=\omega r \end{align}\)
Kulmanopeus voidaan kirjoittaa myös pyörimisnopeuden \(n\) avulla:
\(\omega = 2 \pi n= \dfrac{2 \pi}{T}\)
\([n]=1 \frac{1}{\text{s}} \qquad \text{(rps = revolutions per second)}\)
Kulmakiihtyvyys ja tangenttikiihtyvyys
\(\begin{align} a_t&=\dfrac{\Delta v}{\Delta t} \\ a_t&=\dfrac{r \Delta \omega}{\Delta t} \\ a_t&=\alpha r \end{align}\)
Etenemisliikkeen ja pyörimisliikkeen vertailua
\(\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{|l|l|l|l|} \hline & \textbf{Etenemisliike} & \textbf{Pyörimisliike} \\ \hline & \text{Paikka } x & \text{Kiertokulma } \varphi \\ \hline & \text{Siirtymä } \Delta x & \text{Kiertymä } \Delta \varphi \\ \hline & \text{Nopeus } v=\frac{\Delta x}{\Delta t} & \text{Kulmanopeus } \omega=\frac{\Delta \varphi}{\Delta t} \\ \hline & \text{Kiihtyvyys } a=\frac{\Delta v}{\Delta t} \phantom{\Big|} & \text{Kulmakiihtyvyys } \alpha = \frac{\Delta \omega}{\Delta t}\\ \hline \begin{array}{c} \text{Tasainen} \\ \text{liike}\end{array}&x=x_0+v_0 t & \varphi = \varphi_0 + \omega_0 t \\ \hline \begin{array}{c} \text{Kiihtyvä} \\ \text{liike}\end{array}&x=x_0+v_0 t+\frac{1}{2} at^2 & \varphi = \varphi_0 + \omega_0 t+\frac{1}{2} \alpha t^2 \\ \hline\end{array}\)
Esimerkit
Esimerkki
Levysoittimessa vinyylilevy pyörii tasaisesti pyörimisnopeudella 45 rpm.
Levysoitin saavuttaa pyörimisnopeutensa 2,5 sekunnin kuluttua käynnistämisestä.
a) Laske levyn keskimääräinen kulmakiihtyvyys
b) Kuinka suuri on levyn kiertymä 2,5 sekunnin kuluttua levysoittimen käynnistyksestä?
Ratkaisu a-kohtaan
Kirjataan lähtöarvot
\(\Delta t=2,5 \text{ s}, \ \omega_0 = 0 \text{ rad/s} \\ n=45 \text{ rpm}=\dfrac{45}{60} \dfrac{1}{\text{s}}=\dfrac{3}{4} \dfrac{1}{\text{s}}\)
Muutetaan pyörimisnopeus kulmanopeudeksi.
\(\begin{align} \omega_1 &= 2 \pi n \\ \omega_1 &=2 \pi \cdot \dfrac{3}{4} \dfrac{1}{\text{s}} \\ \omega_1&\approx 4,712 \text{ rad/s} \end{align}\)
Lasketaan keskimääräinen kulmakiihtyvyys
\(\begin{align}\alpha_k&=\dfrac{\Delta \omega}{\Delta t} \\ \alpha_k&=\dfrac{\omega_1-\omega_0}{\Delta t} \\ \alpha_k&=\dfrac{4,712 \text{ rad/s}-0 \text{ rad/s}}{2,5 \text{ s}} \\ \alpha_k & \approx 1,9 \text{ rad/s}^2 \end{align}\)
Vastaus: Keskimääräinen kulmakiihtyvyys on noin \(1,9 \text{ rad/s}^2\)
Ratkaisu b-kohtaan
Oletetaan, että levy on tasaisesti kiihtyvässä pyörimisliikkeessä.
Lasketaan levyn kiertymä
\(\begin{align} \Delta \varphi&=\dfrac{1}{2}\alpha t^2 \\ \Delta \varphi &=\dfrac{1}{2} \cdot 1,885 \text{ rad/s}^2 \cdot (2,5 \text{ s})^2 \\ \Delta \varphi & \approx 5,9 \text{ rad} \end{align}\)
Vastaus: Levyn kiertymä on noin 5,9 radiaania.
Esimerkki
Tietokoneen kiintolevyn pyörimisnopeus 7200 rpm.
Kiintolevyn halkaisija on 2,5 tuumaa.
Laske kiintolevyn ulkoreunassa olevan tarran ratanopeus.

Ratkaisu
Kirjataan lähtöarvot \(n=7200 \text{ rpm}, \ d=2,5"\)
Muutetaan tuumat metreiksi.
\(1" = 0,0254 \text{ m}\)
\(r=\dfrac{d}{2}=\dfrac{2,5"}{2}=1,25"\)
\(r=1,25 \cdot 0,0254 \text{ m}\)
\(r=0,03175 \text{ m}\)
Muutetaan pyörimisnopeus kulmanopeudeksi.
\(\omega = 2 \pi n \)
\(\omega = 2 \pi \cdot \dfrac{7200}{60} \dfrac{1}{\text{s}}\)
\(\omega \approx 754 \text{ rad/s}\)
Lasketaan ratanopeuden suuruus.
\(v=\omega r\)
\(v=754 \text{ rad/s} \cdot 0,03175 \text{ m}\)
\(v \approx 24 \text{ m/s}\)
