Pyöriminen
1,8 metriä korkea tolppa kaatuu maahan.
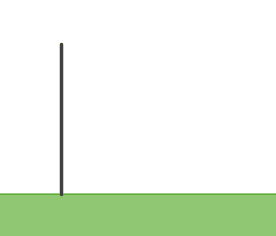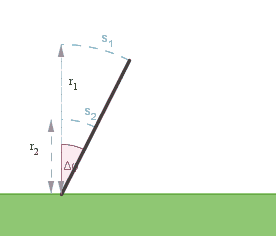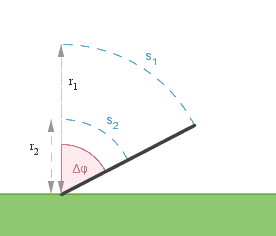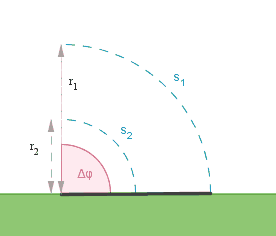
Kuinka pitkän matkan tolpan huippu liikkuu? Entä tolpan keskikohta?
Kirjataan lähtöarvot
\(\Delta \varphi = \dfrac{\pi}{2} \text{ rad}\)
\(r_1 = 1,8 \text{ m} \\ r_2 = 0,9 \text{ m}\)
Tolpan kulkema matka saadaan laskettua radiaanin määritelmän avulla.
\(\Delta \varphi = \dfrac{s}{r}\), josta \(s=r \Delta \varphi\). \(\color{red}{\text{(+3p)}}\)
Sijoitetaan lukuarvot ja lasketaan matkat.
\(s_1=1,8 \text{ m} \cdot \dfrac{\pi}{2} \approx 2,8 \text{ m}\) \(\color{red}{\text{(+1p)}}\)
\(s_2=0,9 \text{ m} \cdot \dfrac{\pi}{2} \approx 1,4 \text{ m}\) \(\color{red}{\text{(+1p)}}\)
Vastaus: Tolpan huippu kulkee 2,8 metriä ja keskikohta 1,4 metriä. \(\color{red}{\text{(+1p)}}\)
Rulettipyödän kiekko kiihtyy levosta kulmanopeuteen 2,50 rad/s 8,0 sekunnissa.
a) Mikä on ruletin keskimääräinen kulmakiihtyvyys?
b) Kuinka suuren kiertymän ruletti tekee tänä aikana?

Kirjataan lähtöarvot
\(\omega_0 = 0,0 \text{ rad/s}, \ \omega_1 = 2,50 \text{ rad/s}, \\ \Delta t=8,0 \text{ s}\)
a) Kulmakiihtyvyys määritellään
\(\begin{align} \alpha_k &= \dfrac{\Delta \omega}{\Delta t} \qquad &&\color{Red}{\text{(+1p)}} \\ \alpha_k &=\dfrac{2,50 \text{ rad/s} - 0,0 \text{ rad/s}}{8,0 \text{ s}} \qquad &&\color{Red}{\text{(+1p)}}\\ \alpha_k & =0,3125 \text{ rad/s}^2 \\ \alpha_k & \approx 0,31 \text{ rad/s}^2 \end{align}\)
Vastaus: Ruletin keskimääräinen kulmakiihtyvyys on noin \(0,31 \text{ rad/s}^2\) \(\color{Red}{\text{(+1p)}}\)
b) Oletetaan, että ruletti on tasaisesti kiihtyvässä liikkeessä.
Nyt voidaan laskea ruletin kiertymä.
\(\begin{align} \Delta \varphi &= \dfrac{1}{2}\alpha t^2 \qquad &&\color{Red}{\text{(+1p)}}\\ \Delta \varphi &=\dfrac{1}{2} \cdot 0,3125 \text{ rad/s}^2 \cdot \Big( 8,0 \text{ s}\Big)^2 \qquad &&\color{Red}{\text{(+1p)}} \\ \Delta \varphi &= 10 \text{ rad} \end{align} \)
Vastaus: Ruletin kiertymä 8,0 sekunnin aikana on 10 radiaania. \(\color{Red}{\text{(+1p)}}\)
DVD-soittimen levy ei pyöri tasaisesti, vaan pyörimisnopeus vaihtelee välillä 1530 - 630 rpm. Levyn pyörimisnopeus on suurin, kun DVD-soittimen lukija lukee levyn sisäkehää ja pienin, kun lukija lukee levyn ulkokehää. DVD-soitin aloittaa levyn lukemisen sisäkehältä, tasaisesti hidastaen pyörimistään lähestyessään ulkokehää.
Mikä on DVD-levyn keskimääräinen kulmakiihtyvyys, jos soittimen sisällä on "Blade runner" -elokuva vuodelta 1982, jonka kokonaiskesto on 116 minuuttia?

Kirjataan lähtöarvot
\(n_0=1530 \text{ rpm}, \ n_1=630 \text{ rpm}, \\ t=116 \text{ min}\)
Kulmakiihtyvyys määritellään
\(\begin{align} \alpha_k &= \dfrac{\Delta \omega}{\Delta t} \quad &&||\omega=2 \pi n \ \color{Red}{\text{(+2p)}} \\ \alpha_k&=\dfrac{2 \pi n_1 - 2 \pi n_0}{\Delta t} \\ \alpha_k &=\dfrac{2 \pi(n_1-n_0)}{\Delta t} \\ \alpha_k&=\dfrac{2 \pi \Big(\frac{630}{60} \frac{1}{\text{s}}-\frac{1530}{60}\frac{1}{s} \Big)}{116 \cdot 60 \text{ s}} &&\color{Red}{\text{(+2p)}} \\ \alpha_k& \approx - 0,014 \text{ rad/s}^2 \end{align}\)
Vastaus: DVD-levyn kulmakiihtyvyys on noin \(-0,014 \text{ rad/s}^2\) \(\color{Red}{\text{(+2p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
