FY5: Pyörimisen liikeyhtälö ja energia

Teoria

Hitausmomentti

Mitataan valoportin avulla rakolevyn kulmanopeutta, kun muutetaan rakolevyyn vaikuttavan momentin suuruutta.

\((t, \ \omega)-\)koordinaatistoon piirretyn suoran fysikaalinen kulmakerroin on rakolevyn kulmakiihtyvyys.

 

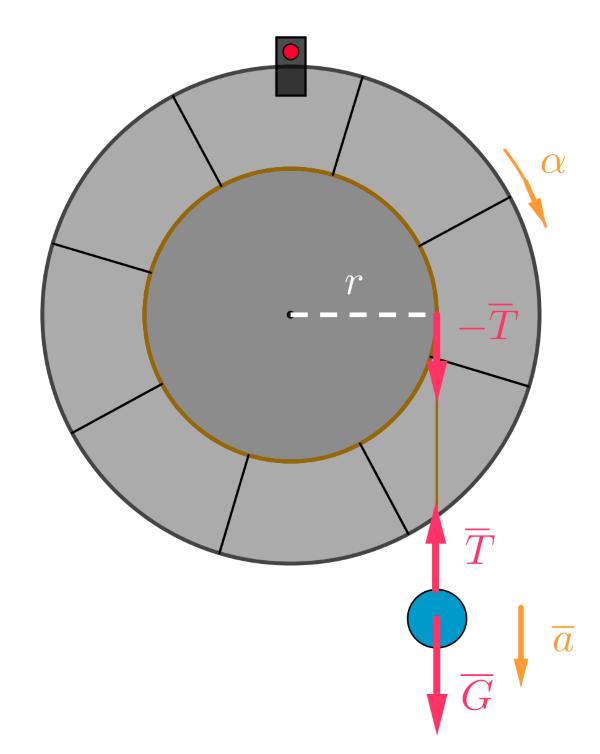
Tarkastellaan punnuksen liikeyhtälöä. Newtonin 2. lain mukaan

\(\begin{align}\sum \overline{F}&=m\overline{a} \\ \overline{G}+\overline{T}&=m\overline{a} \\ G-T&=ma \\ T &=mg - ma \end{align} \)

Mittaus toteutetaan pienillä punnuksilla, jolloin punnuksen kiihtyvyydet ovat pieniä, joten
 \(T \approx mg\).
 
Vastaavasti rakolevyyn kohdistuva momentti on
\(\begin{align}M &=Tr \\ M&\approx mgr. \end{align}\)
 
Langan etäisyys kiertoakselista on 2,0 cm. Mitataan punnuksen massa ja rakolevyn kulmakiihtyvyys. 
Lasketaan langan jännitysvoima (\(T \approx mg\)) ja rakolevyyn kohdistuvan momentin suuruus (\(M \approx mgr\))
\(\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{|c|c|c|c|} \hline m\ \text{(kg})& \alpha \ \text{(rad/s}^2) & T \text{ (N)} & M \text{ (Nm)}\\ \hline 0,014& 0,552 & 0,137 & 0,00275\\ \hline 0,017& 0,636 & 0,167 &0,00334 \\ \hline 0,020&0,754 & 0,196 & 0,00392\\ \hline0,022&0,837& 0,216 & 0,00432\\ \hline 0,030& 1,16 &0,294 & 0,00589 \\ \hline 0,036 & 1,40 & 0,353 & 0,00706 \\ \hline\end{array}\)
 
Sijoitetaan mittaustulokset \((\alpha, \ M)-\)koordinaatistoon.

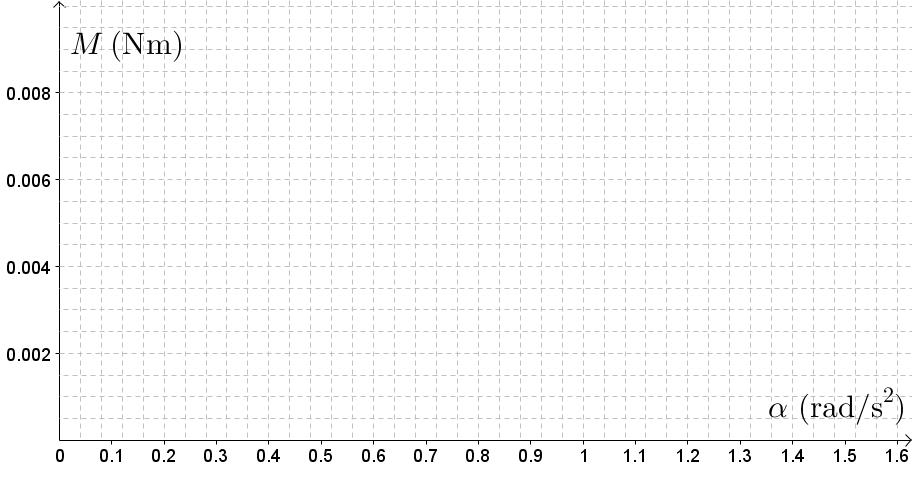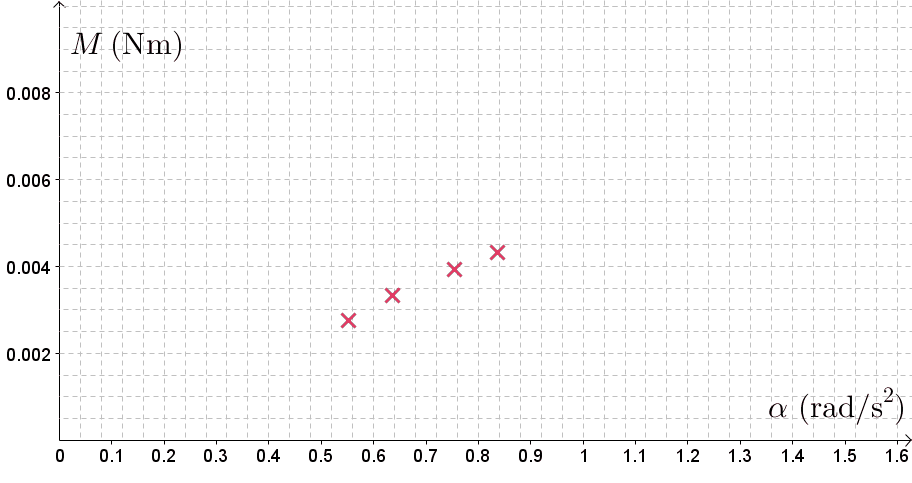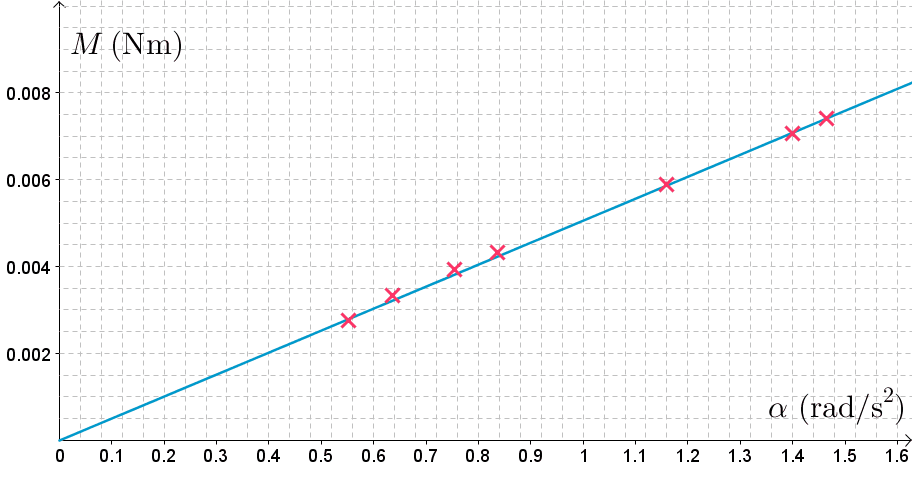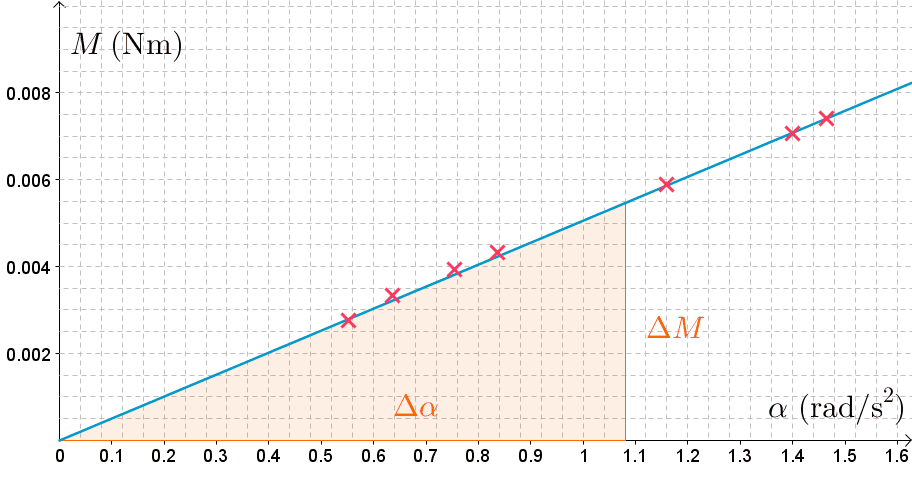
Kuvaajasta huomataan, että momentti ja kulmakiihtyvyys ovat suoraan verrannollisia.

Suoran fysikaalinen kulmakerroin on rakolevyn hitausmomentti.

\(J=\dfrac{\Delta M}{\Delta \alpha}=\dfrac{0,0055 \text{ Nm}}{1.08 \text{ rad/s}^2} \approx 0,0051 \text{ Nms}^2 \)

\(J= 0,0051 \text{ kgm}^2\)

 

Kappaleen hitausmomentit kuvaa kappaleen kykyä vastustaa pyörimisliikkeen muutosta tietyn akselin suhteen.

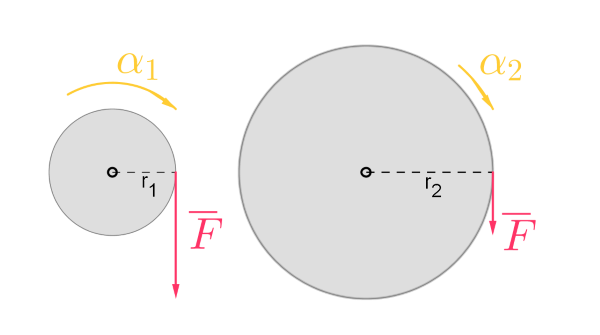
Jos molempiin kappaleisiin vaikuttaa yhtä suuri momentti, niin kappaleella jolla on pienempi hitausmomentti on suurempi kulmakiihtyvyys.

 

Pyörimisen liikeyhtälö

\(\sum M=J\alpha\)

\(\sum M \) on kappaleeseen kohdistuvien momenttien summa.

\(\alpha \) on kappaleen kulmakiihtyvyys.

\(J\) on kappaleen hitausmomentti.

 

\(\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{|c|c|c|} \hline \text{Kappale}& \text{Etenemisliike} & \text{Pyörimisliike} \\ \hline \text{liikeyhtälö}& \sum \overline{F}=m\overline{a} & \sum M = J \alpha\\ \hline\text{kohdistuu}& F & M \\ \hline \text{havaitaan}& a & \alpha \\ \hline \text{vastustaa}&m & J \\ \hline\end{array}\)

 

Videot