Teoria
Rotaatioenergia
Levy pyörii tasaisella kulmanopeudella \(\omega\) akselin A suhteen.
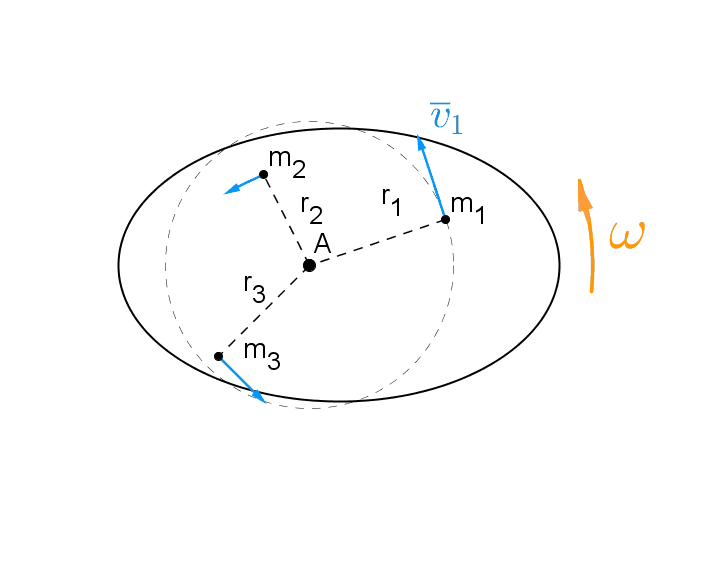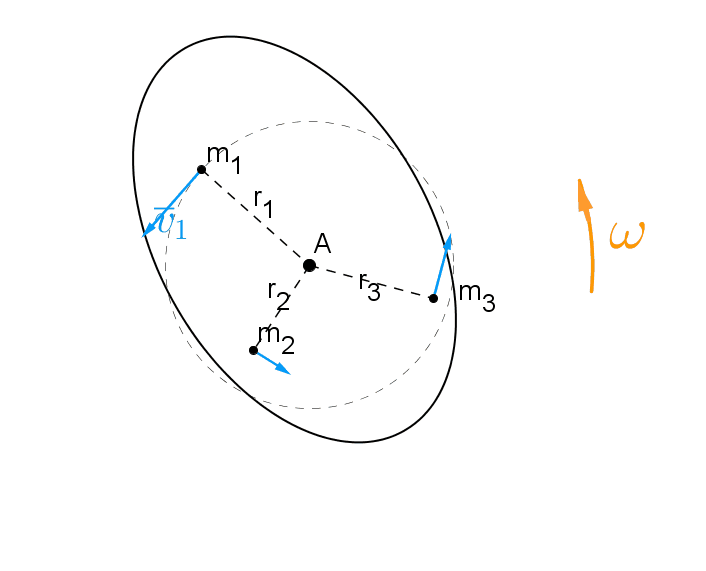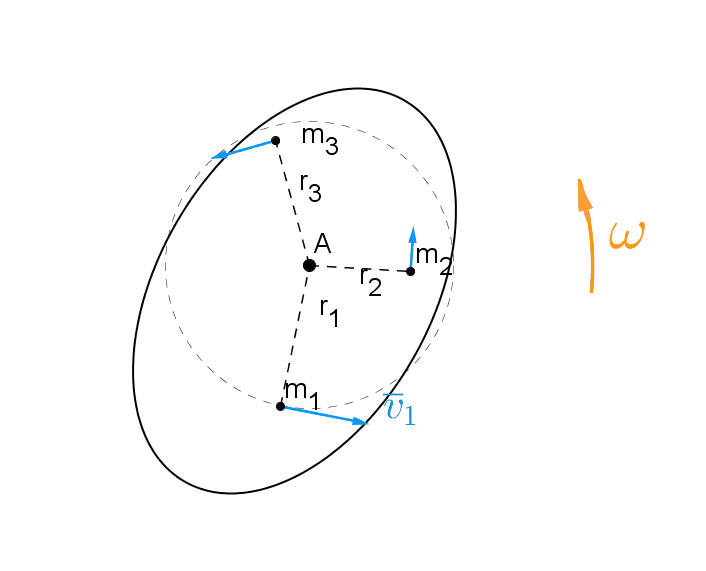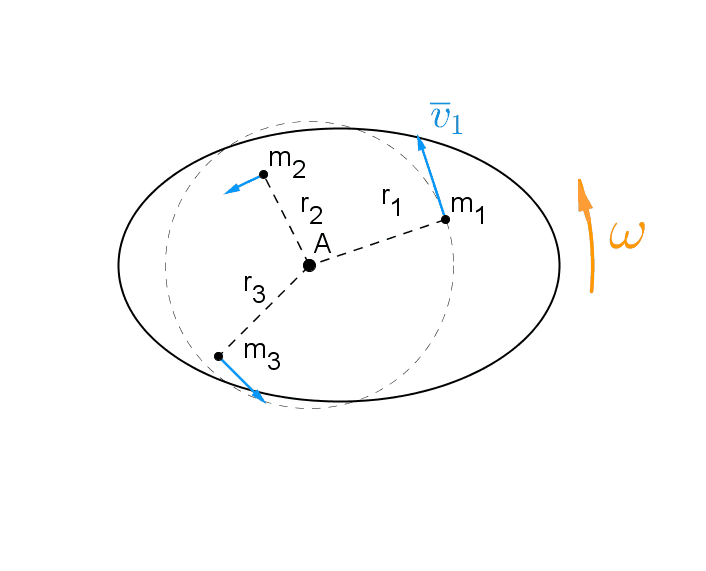
Levy koostuu yksittäisistä massapisteistä
\(m_1, \ m_2, \ m_3, \ \ldots\)
Pyörivän kappaleen liike-energia on näiden pisteiden liike-energian summa.
\(E_r = \dfrac{1}{2}m_1v_1^2+\dfrac{1}{2}m_2v_2^2+\dfrac{1}{2}m_3v_3^2+ \ldots\)
Jokainen massapiste pyörii samalla kulmanopeudella \(\omega\).
Ratanopeuden ja kulmanopeuden välinen yhteys on \(v=r\omega \).
\(E_r = \dfrac{1}{2}m_1( r_1\omega)^2+\dfrac{1}{2}m_2(r_2\omega)^2+\dfrac{1}{2}m_3( r_3\omega)^2+ \ldots\)
\(E_r = \dfrac{1}{2}m_1r_1^2\omega^2+\dfrac{1}{2}m_2r_2^2\omega^2+\dfrac{1}{2}m_3r_3^2\omega^2+ \ldots \qquad ||\text{yhteinen tekijä}\)
\(E_r = \dfrac{1}{2}\Big(m_1r_1^2+\dfrac{1}{2}m_2r_2^2+\dfrac{1}{2}m_3r_3^2+ \ldots\Big) \omega^2\)
\(E_r = \dfrac{1}{2}\Big(\sum m_ir_i^2\Big) \omega^2\)
Summa \(\sum m_ir_i^2\) on kappaleen hitausmomentti \(J\).
Pyörivän kappaleen rotaatioenergia eli pyörimisenergia saadaan kirjoitettua muotoon:
\(E_r = \dfrac{1}{2}J \omega^2\)
Vieriminen
Yleisesesti kappaleen massakeskipisteen liike ja pyörimisliike ovat toisistaan riippumattomia.
Viermisliikkeessä etenemisliikkeen ja pyörimisliikkeen välillä on riippuvus.
Kiertokulmaa vastaavan ympyräkaaren pituus on sama kuin kappaleen etenemä matka.
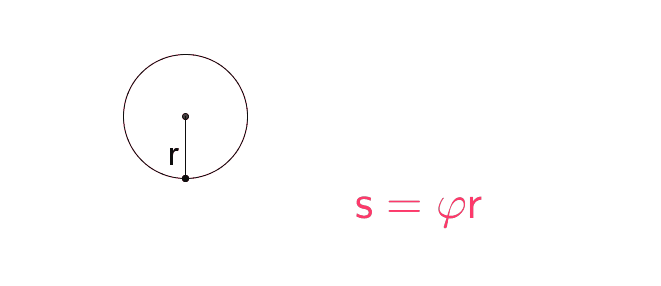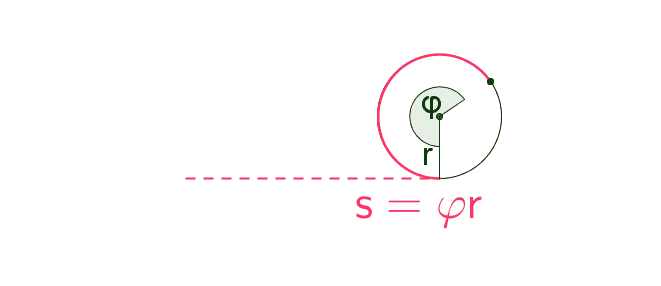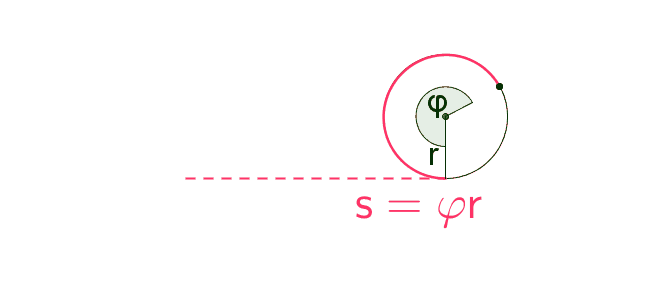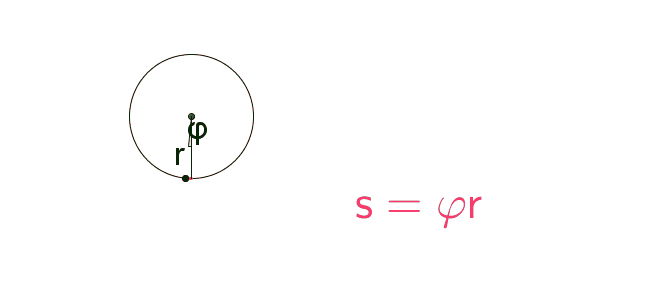
\(\begin{align} \qquad s &= \varphi r \\ \Rightarrow v & =\omega r \\ \Rightarrow a & = \alpha r \end{align}\)
Jos kappale vierii (eikä luista), niin vierimisehto eli \(v=\omega r\) toteutuu.
Kappaleen vieriessä pinnan ja kappaleen välinen lepokitka aiheuttaa kappaleelle momentin.
Renkaan pyörimisen liikeyhtälö
\(\begin{align} \sum M &= J \alpha \\ F_{\mu 0}r &= J \alpha \end{align} \)
Lepokitkakerroin \(\mu_0\) asettaa ylärajan kappaleen kulmakiihtyvyydelle vierimisessä,.
Jos pyörivää kappaletta vedetään tai työnnetään liian suurella voimalla, niin kappale liukuu.
Tällöin vierimisehto ei toteudu ja \(a \neq \alpha r\).
Mekaanisen energian säilyminen
\(\begin{align} E_0 &= E_1 \\ mgh_0 + \dfrac{1}{2}mv_0^2+\dfrac{1}{2}J\omega_0^2 & =mgh_1+\dfrac{1}{2}mv_1^2+\dfrac{1}{2}J\omega_1^2 \end{align}\)
Videot
Esimerkit
Umpinaisen sylinterin muotoinen kappale vierii alas 1,50 metriä korkeaa mäkeä.
Kuinka suuri on sylinterin loppunopeus mäen alaosassa?
Ratkaisu
Kirjataan lähtöarvot \(h=1,5 \text{ m}\).
Oletetaan, että sylinterin mekaaninen energia säilyy.
Sylinterin potentiaalienergia muuttuu sylinterin liike- ja pyörimisenergiaksi.
\(\begin{align} E_0&=E_1 \\ mgh&=\dfrac{1}{2}mv^2+\dfrac{1}{2}J\omega^2 \end{align}\)
Koska sylinteri vierii, niin vierimisehto \(v=\omega r\) toteutuu.
Umpinaisen sylinterin hitausmomentti on \(J=\dfrac{1}{2}mr^2\)
.\(\begin{align} mgh&=\dfrac{1}{2}mv^2+\dfrac{1}{2}J\omega^2 \\ mgh&=\dfrac{1}{2}mv^2+\dfrac{1}{2} \cdot \dfrac{1}{2}mr^2 \cdot \Big( \dfrac{v}{r} \Big) ^2 \\ mgh&=\dfrac{1}{2}mv^2 + \dfrac{1}{4}mr^2 \cdot \dfrac{v^2}{r^2} \\ mgh&=\dfrac{1}{2}mv^2+\dfrac{1}{4}mv^2 \\ gh&=\dfrac{1}{2}v^2+\dfrac{1}{4}v^2 \\ 4gh&=2v^2+v^2 \\ v^2&=\dfrac{4gh}{3} \\ v&=\sqrt{\dfrac{4gh}{3}} \end{align}\)
Sijoitetaan tunnetut lukuarvot
\(v=\sqrt{\dfrac{4 \cdot 9,81 \text{ m/s}^2 \cdot 1,5 \text{ m}}{3}}\)
\(v \approx 4,4 \text{ m/s}\)
Vastaus: Sylinteri vierii rampin alapäähän nopeudella 4,4 m/s.
