Rotaatioenergia
a) Mitä tarkoittaa, että kappale vierii?
b) Umpinainen sylinteri vierii alas kaltevaa tasoa. Piirrä sylinterin voimakuvio ja nimeä sylinteriin kohdistuvat voimat.
a) Vierimisessä kappale pyörii ja etenee samanaikaisesti sillä ehdolla, että kappale ei liu'u pinnan suhteen. \(\color{Red}{\text{(+1p)}}\)
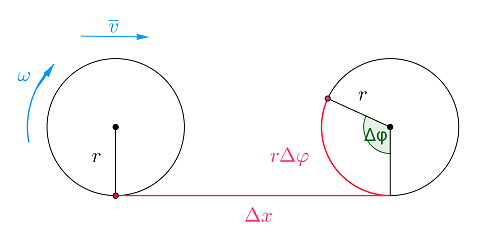
Kappaleen vieriessä kappaleen painopisteen etenemisnopeus ja kappaleen kulmanopeus toteuttavat ehdon \(v=\omega r\). \(\color{Red}{\text{(+1p)}}\)
Kappaleen saa vierimään kappaleen ja pinnan välinen lepokitkan momentti. \(\color{Red}{\text{(+1p)}}\)
b) Sylinteri vierii alas kaltevaa tasoa. Piirretään sylinterin voimakuvio.
\(\color{Red}{\text{(Kuvio oikein +1,5 p)}}\)
\(N \text{ pinnan tukivoima } \\ G \text{ sylinteriin kohdistuva paino} \\ F_{\mu 0} \text{ lepokitka}\)
\(\color{Red}{\text{(+0,5p/voima)}}\)
Lepokitka aiheuttaa sylinteriin momentin, joka aiheuttaa sylinterin vierimisen.
Oletetaan maapallo homogeeniseksi palloksi, joka kiertää Aurinkoa ympyrärataa.
Kuinka suuri on maapallon liike-energia rataliikkeessä Auringon ympäri?
Kuinka suuri on maapallon pyörimisenergia oman akselinsa ympäri?
Etsitään taulukkokirjasta tai internetistä seuraavat lähtöarvot:
\(\begin{align} &\text{Maapallon radan säde} &&s =149,597 \cdot 10^{9} \text{ m} \\ &\text{Maapallon massa} &&m=5,9737 \cdot 10^{24} \text{ kg} \\ &\text{Maapallon säde} &&r=6371 \cdot 10^3 \text{ m} \\ &\text{Kiertoaika Auringon ympäri} &&T=365 \text{ d} \\ &\text{Maapallon keskinopeus radalla } &&v=29,78 \cdot 10^3 \text{ m/s} \\ &\text{Pyörähdysaika akselinsa ympäri }&& t=24 \text{ h} \end{align}\)
\(\color{Red}{\text{(Lähtöarvot etsitty/laskettu +1p)}}\)
Oletetaan, että maapallo kiertää Aurinkoa pitkin ympyrärataa. Tällöin maapalloon kohdistuva gravitaatiovoima kohdistuu kohti ympyräradan keskipistettä ja on kohtisuorassa maapallon ratanopeutta vastaan.
Nyt gravitaatiovoima ei muuta maapallon ratanopeuden suuruutta, vaan pelkästään sen suuntaa.
Maapallon kiertoliikkeen liike-energia Auringon suhteen.
\(\begin{align} E_k&=\dfrac{1}{2}mv^2 \qquad &&\color{Red}{\text{(+1p)}}\\ E_k&=\dfrac{1}{2} \cdot 5,9737 \cdot 10^{24} \text{ kg} \cdot (29,78 \cdot 10^3\text{ m/s})^2 &&\color{Red}{\text{(+1p)}}\\ E_k&=2,6488831 \cdot 10^{33} \text{ J} \\ E_k&\approx 2,65 \cdot 10^{33} \text{ J} \end{align}\)
Maapallon pyörimisenergia oman akselinsa suhteen.
\(\begin{align} E_r&=\dfrac{1}{2}J \omega^2 \qquad &&||J=\frac{2}{5}mr^2, \ \omega=\frac{2\pi}{t} \\ E_r&=\dfrac{1}{2} \cdot \dfrac{2}{5}mr^2 \cdot \Big( \dfrac{2\pi}{t}\Big)^2 &&\color{Red}{\text{(+1p)}}\\ E_r&=\dfrac{1}{2}\cdot \dfrac{2}{5} \cdot 5,9737 \cdot 10^{24} \text{ kg} \cdot (6,371 \cdot 10^6 \text{ m})^2 \cdot \Big(\dfrac{2 \pi } {24 \cdot 60 \cdot 60}\Big)^2 &&\color{Red}{\text{(+1p)}}\\ E_r &=2,564607 \cdot 10^{29} \text{ J} \\ E_r & \approx 2,56 \cdot 10^{29} \text{ J}\end{align}\)
Vastaus: Kiertoliikkeen liike-energia on noin \(2,65 \cdot 10^{33} \text{ J}\) ja pyörimisliikkeen energia noin \(2,56 \cdot 10^{29} \text{ J} \ \color{Red}{\text{(+1p)}}\).

Toisen tauluviivaimen päähän on kiinnitetty raskas punnus.
a) Kummalla tauluviivaimista on suurempi kulmakiihtyvyys heti irrotuksen jälkeen? Perustele (1p)
b) Kuinka suurella nopeudella pelkkä viivain osuu maahan? (5p)
Ratkaisu a-kohtaan.
Kappaleen hitausmomentti määritellään \(J=\sum m_i r_i^2\).
Pelkän viivaimen hitausmomentti
\(J_1=\dfrac{1}{3}m_vr^2\)
Viivaimen ja punnuksen hitausmomentti.
\(J_2=J_1 +m_pr^2\)
\(J_2=\dfrac{1}{3}m_vr^2+m_pr^2\)
Viivaimen ja punnuksen muodostaman systeemin hitausmomentti on suurempi kuin pelkän viivaimen hitausmomentti. \(\color{Red}{\text{(+0,5p)}}\)
Hitausmomentti kuvaa kappaleen kykyä vastustaa pyörimisliikkeen muutosta tietyn akselin suhteen.
Pelkällä viivaimella on suurempi kulmakiihtyvyys. \(\color{Red}{\text{(+0,5p)}}\)
Ratkaisu b-kohtaan
Kirjataan lähtöarvot
\(L=1,0 \text{ m},\ g=9,81 \text{ m/s}^2\)
Oletetaan, että mekaaninen energia säilyy. \(\color{Red}{\text{(+1p)}}\)
Tarkastellaan viivainta homogeenisena tankona.
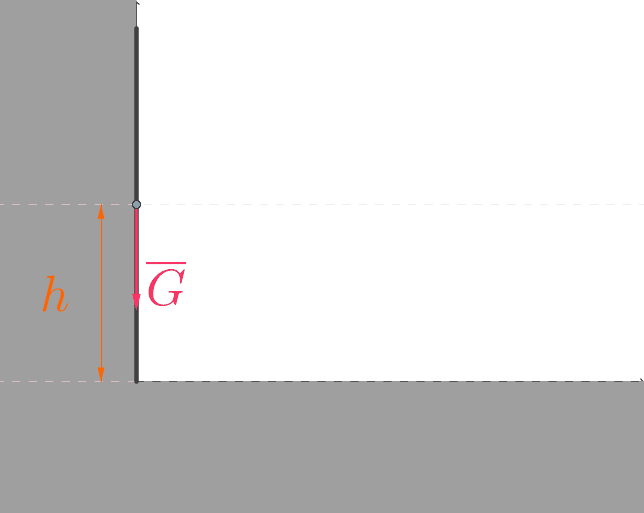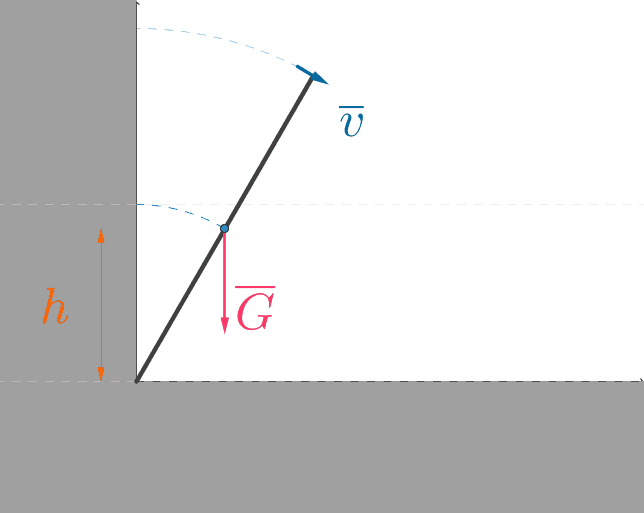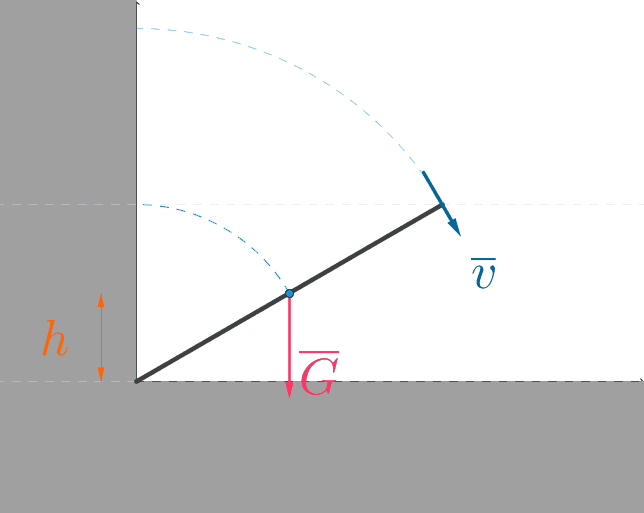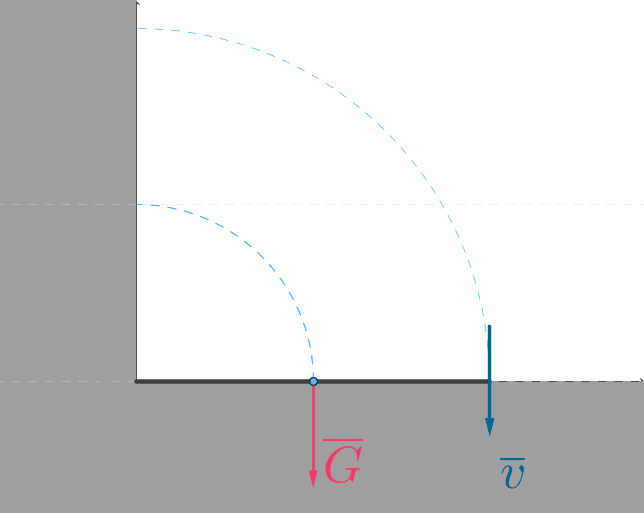
Alkutilanne
Aluksi viivaimella on vain potentiaalienergiaa.
Viivaimen massakeskipiste on puolessa välissä viivainta, jolloin sen korkeus maasta on \(h=\dfrac{L}{2}\). \(\color{Red}{\text{(+0,5p)}}\)
Viivaimen potentiaalienergia on \(E_p=mgh=\dfrac{1}{2}mgL\).
Lopputilanne
Toisesta päästä pyörivän homogeenisen tangon hitausmomentti on \(J=\dfrac{1}{3}mL^2\).
Tanko on pyörimisliikkeessä, joten tangolla on pyörimisenergiaa.
Lopuksi tangolla on vain pyörimisenergiaa \(E_{r}=\dfrac{1}{2}J\omega^2\). \(\color{Red}{\text{(+0,5p)}}\)
Mekaanisen energian säilymislaista seuraa, että viivaimen potentiaalienergia muuntuu viivaimen pyörimisenergiaksi.
\(\begin{align} E_p& = E_r \\ mgh&=\dfrac{1}{2}J\omega^2 \qquad &&|| h=\frac{L}{2}, \ J=\frac{1}{3}mL^2 \\ \dfrac{1}{2}mgL&=\dfrac{1}{2}\cdot \dfrac{1}{3}mL^2 \omega^2 &&||:\frac{1}{2}m\\ gL&=\dfrac{1}{3}L^2\omega^2 &&||:\frac{1}{3}L^2 \\ \dfrac{3g}{L}&=\omega^2 &&||\sqrt{} \\ \omega&=\sqrt{\dfrac{3g}{L}} && \color{Red}{\text{(+1p)}} \end{align}\)
Sijoitetaan lukuarvot.
\(\omega = \sqrt{\dfrac{3 \cdot 9,81 \text{ m/s}^2}{1,0 \text{ m}}} \\ \omega \approx 5,42 \text{ rad/s}\)
Lasketaan vielä viivaimen ratanopeus.
\(v=\omega r \\ v=5,42 \text{ rad/s} \cdot 1,0 \text{ m}\qquad \color{Red}{\text{(+1p)}} \\ v\approx 5,4 \text{ m/s}\)
Vastaus: Viivain osuu lattiaan nopeudella 5,4 m/s. \(\color{Red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
