Teoria
Vektorien summa
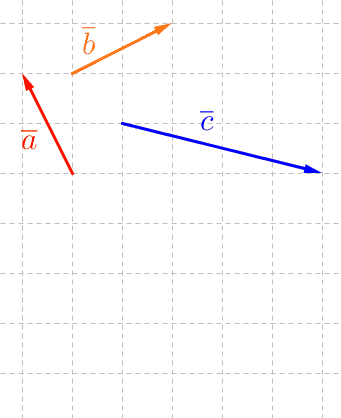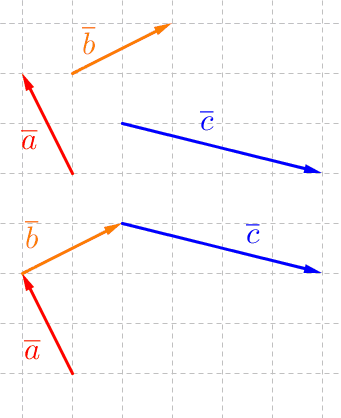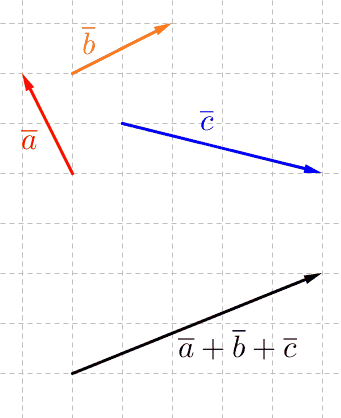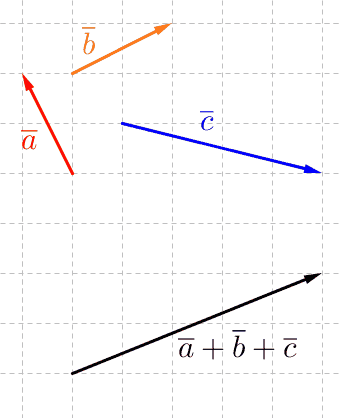
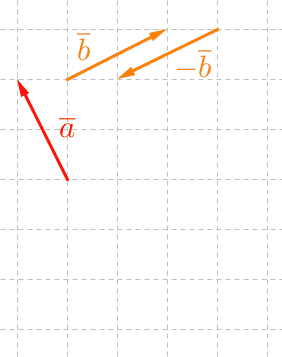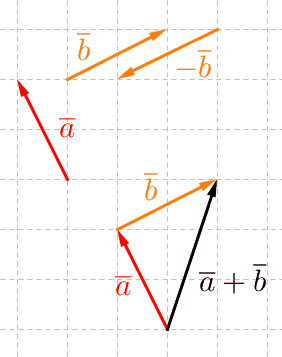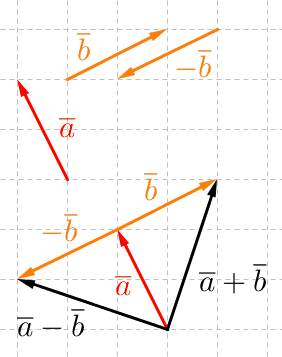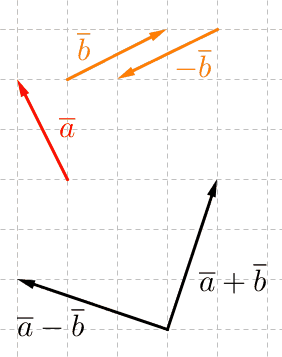
Summavektori (esim. \(\overline a+\overline b+ \overline c\)) saadaan yhdistämällä vektorit siten, että seuraava vektori alkaa siitä pisteestä, mihin edellinen päättyy. Summavektorin alkupiste on ensimmäisen vektorin alkupiste ja loppupiste on viimeisen vektorin loppupiste.
Vektorien erotus
Vektorien $\overline a$ ja $\overline b$ erotus voidaan ajatella vektorien $\overline a$ ja $-\overline b$ summavektorina:
\(\overline a+(-\overline b)=\overline a-\overline b\)
Vektorin ja reaaliluvun tulo
\(\begin{align} &2 \cdot \overline a=\overline a+\overline a=2\overline a\\ &-3\cdot\overline a=(-\overline a)+(-\overline a)+(-\overline a)=-3\overline a \end{align}\)
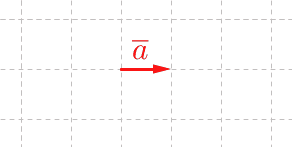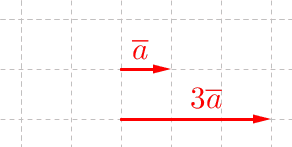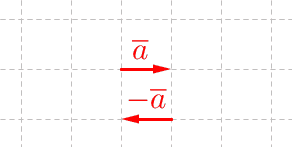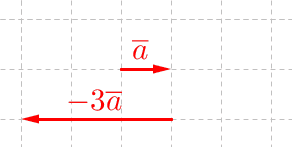
Vektori \(2 \overline a\) on samansuuntainen kuin vektori \(\overline a\), mutta pituudeltaan kaksinkertainen (eli \(2\overline a \uparrow \uparrow \overline a\) ja \(| 2 \overline a|=2\cdot |\overline a|\)). Vektori \(-3 \overline a\) on vastakkaissuuntainen ja pituudeltaan kolminkertainen vektoriin \(\overline a\) verrattuna (eli \(-3\overline a \uparrow \downarrow \overline a\) ja \(| -3 \overline a|=3\cdot |\overline a|\)).
Vektorin komponentit
Jos tason vektorit \(\overline a\) ja \(\overline b\) ovat keskenään erisuuntaiset \((\overline a \not\parallel \overline b)\), eli vektorit ovat tason kanta, niin niiden avulla pystytään esittämään mikä tahansa muu saman tason vektori.
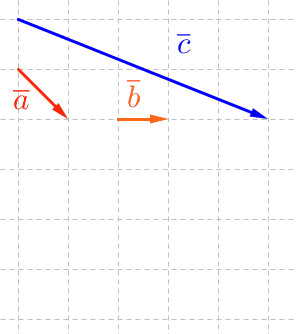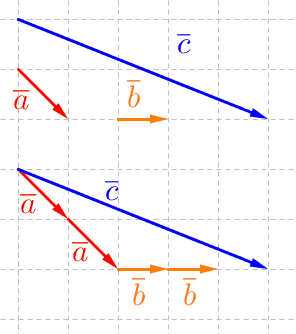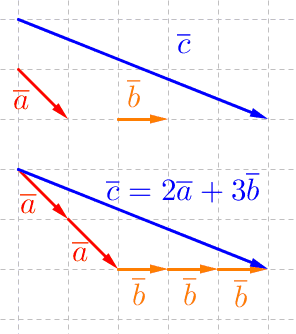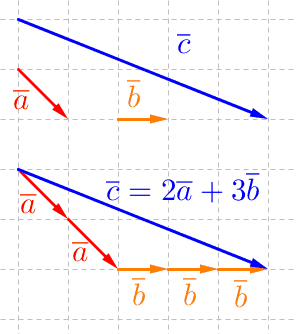
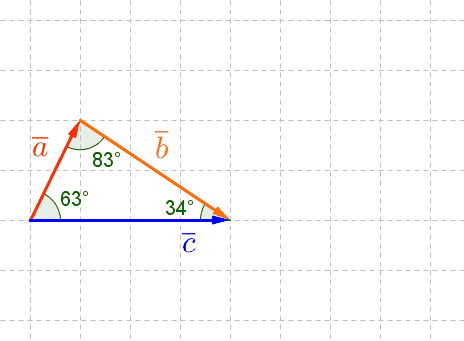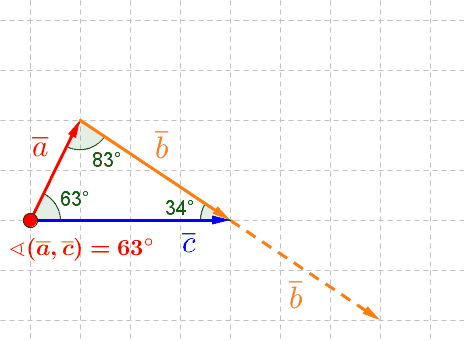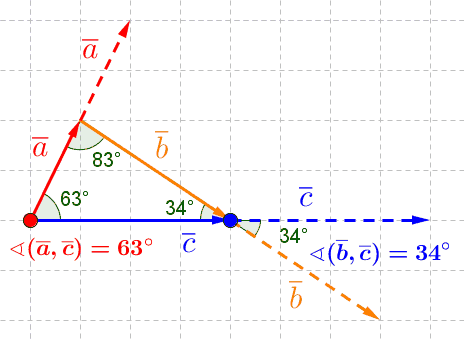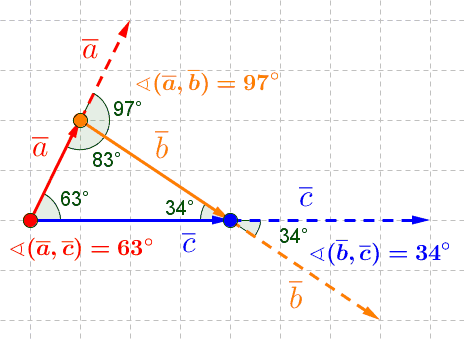
Vektorien välinen kulma
Vektorien välinen kulma on pienempi niistä kahdesta kulmasta, jotka muodostuvat, kun vektorit siirretään alkamaan samasta pisteestä.