heijastuminen ja taittuminen
a) Mitä tarkoittaa kokonaisheijastuminen? Milloin kokonaisheijastuminen voi tapahtua?
b) Laske valon kokonaisheijastumisen rajakulma ilma-lasi-aineparille.
Ratkaisu a-kohtaan.
Kokonaisheijastumisessa kahden aineen rajapintaan saapuva aalto heijastuu täydellisesti, eikä taitu. \(\color{Red}{\text{(+1p)}}\)
Kokonaisheijastuminen tapahtuu, kun aaltoliike saapuu aineiden rajapintaan kriittisen kulman (kokonaisheijastumisen rajakulman) ylittävässä kulmassa pinnan normaalin suhteen. \(\color{Red}{\text{(+1p)}}\)
Kokonaisheijastuminen on mahdollista vain, jos aalto saapuu aalto-opillisesti tiheämmästä aineesta harvempaan. \(\color{Red}{\text{(+1p)}}\)

Kuvassa valo kokonaisheijastuu lasin ja ilman rajapinnassa.
Ratkaisu b-kohtaan.
Kokonaisheijastuminen voi tapahtua vain, kun valo tulee lasista ilmaan eli optisesti tiheämmästä aineesta optisesti harvempaan.
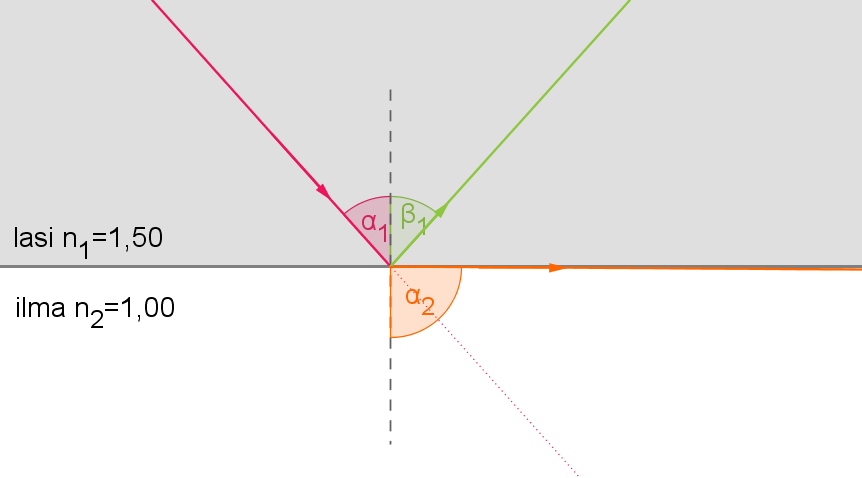
Kokonaisheijastumisen rajatapauksessa taittumiskulma on \(\alpha_2 = 90^{\circ}\).
Taulukkokirjasta saadaan lasin taitekertoimeksi 1,50.
Sovelletaan taittumislakia.
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\dfrac{n_2}{n_1}\) \(\color{Red}{\text{(+1p)}}\)
\(\dfrac{\sin \alpha_1}{\sin 90^{\circ}}=\dfrac{1,00}{1,50}\) \(\color{Red}{\text{(+1p)}}\)
\(\sin \alpha_1=\dfrac{1,00}{1,50}\)
\( \alpha_1 \approx 41,8^\circ\)
Vastaus: Kokonaisheijastumisen rajakulma on 41,8 astetta, kun valo saapuu lasista ilmaan. \(\color{Red}{\text{(+1p)}}\)
Kala on paikoillaan 2,0 metrin syvyydellä.
Minkä kokoiselle alueelle (pinta-ala) veden yläpuolinen maailma kuvautuu kalan yläpuolelle veden pintaan?
Valo tulee kalan yläpuolelta ympyrän muotoiselta alueelta taittuen kalan silmän.
Vedenpinnan yläpuolelta tuleva valo muodostaa suoran ympyräpohjaisen kartion kulkeutuessaan kalan silmään.
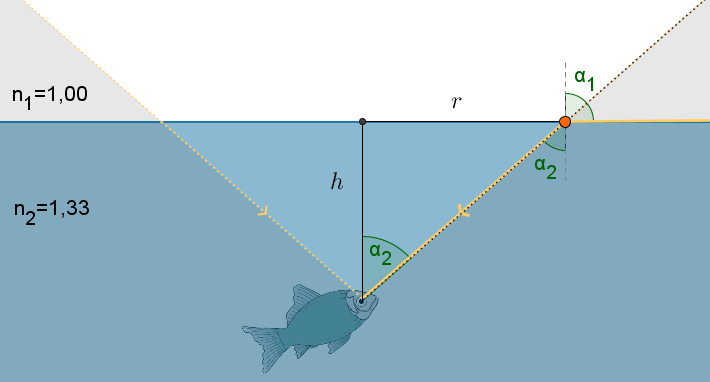
Piirretään kuva tilanteesta.
 e
e
Ratkaistaan valon kokonaisheijastuksen rajakulma \(\alpha_2\), jossa \(\alpha_1=90^{\circ}\). \(\color{Red}{\text{(+1p)}}\)
Taittumislain mukaan
\(\dfrac{\sin \alpha_1}{\sin \alpha_2}=\frac{n_2}{n_1}\) \(\color{Red}{\text{(+1p)}}\)
\(\dfrac{\sin90^{\circ}}{\sin \alpha_2}=\dfrac{1,33}{1}\)
\(\dfrac{1}{\sin \alpha_2}=1,33\)
\(\sin \alpha_2 = \dfrac{1}{1,33}\) \(\color{Red}{\text{(+1p)}}\)
\(\alpha_2 \approx 48,8^\circ\) \(\color{Red}{\text{(+1p)}}\)
Ratkaistaan tämän tiedon avulla ympyräkartion pohjaympyrän säde r.
\(\begin{align}\tan \alpha_2 &= \dfrac{r}{h} \\ r&=h \tan \alpha_2 \end{align}\)
Lasketaan pohjaympyrän pinta-ala.
\(\begin{align}A&= \pi r^2 \\ A&=\pi (h \tan \alpha_2)^2 \\ A&=\pi (2,0 \text{ m} \cdot \tan 48,8^{\circ})^2 \\ A& \approx 16,4 \text{ m}^2 \end{align} \) \(\color{Red}{\text{(+1p)}}\)
Vastaus: Kala näkee noin 16,4 neliömetrin suuruisen, ympyränmuotoisen alueen vedenpinnan yläpuolella. \(\color{Red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
