heijastuminen, taipuminen, resonanssi, diffraktio ja interferenssi
a) Selitä resonanssi eli myötävärähtely
b) Tacoma Narrowsin silta romahti vuonna 1940. Katso oheinen video ja pohdi syitä sillan romahtamiselle.
a) Värähtelijä A on resonanssissa, kun siihen vaikuttaa ulkopuolinen värähtelijä B, jonka taajuus on sama tai lähes sama kuin värähtelijän A ominaisvärähtelytaajuus. Tätä ilmiötä kutsutaan resonanssiksi. \(\color{Red}{\text{(+3p)}}\)
Värähtelijä B siirtää energiaa värähtelijään A sen ominaistaajuudella ja saa sen värähtelemää. Energian siirtyessä värähtelijän A ominaistaajuudella, sen amplitudi kasvaa kasvamistaan.
b) Tacoman silta romahtaminen johtui muun muassa siitä, että tuulen aikaansaamat pyörteet saivat sillan rakenteet värähtelemään sen ominaistaajuudella. \(\color{Red}{\text{(+2p)}}\)
Tuulen jatkuessa sillan värähtelyn amplitudi kasvoi, kunnes lopulta sen rakenteet pettivät. \(\color{Red}{\text{(+1p)}}\)
a) Määrittele interferenssi ja anna esimerkki tapahtumasta jossa havaitaan interferenssi.
b) Määrittele diffraktio ja anna esimerkki tapahtumasta jossa havaitaan diffraktio.
a-kohdan ratkaisu.
Diffraktiossa aallon muoto muuttuu ("taipuu"), kun se kohtaa esteen, esimerkiksi raon. \(\color{Red}{\text{(+1,5p)}}\)
Diffraktio havaitaan esimerkiksi kun vesiaallot kohtaavat aallonmurtajan. \(\color{Red}{\text{(+1,5p)}}\)
b-kohdan ratkaisu.
Interferenssi tarkoittaa kahden aallon yhdistymistä, joiden seurauksena syntyy summa-aalto. \(\color{Red}{\text{(+1,5p)}}\)
Interferenssi voi olla destruktiivista tai konstruktiivista.
Interferenssi havaitaan esimerkiksi kun valkoinen valo heijastuu saippuakuplasta. \(\color{Red}{\text{(+1,5p)}}\)
a) Miksi valo taipuu hilassa? (K89/3)
b) Laservalo, jonka aallonpituus on 633 nm, osuu kohtisuorasti hilaan,
jossa on 340 rakoa millimetrillä. Kuinka monta intensiteettimaksimia saadaan
näkyviin hilan taakse asetetulle varjostimelle?
Ratkaisu a-kohtaan
Kun valo kohdistetaan hilaan, niin valo taipuu eli tapahtuu valon diffraktio. \(\color{Red}{\text{(+1p)}}\)
Tietyissä suunnissa valoaallot vahvistavat ja tietyissä heikentävät toisiaan eli tapahtuu valoaaltojen interferenssi. \(\color{Red}{\text{(+1p)}}\)
Hilassa tapahtuu valon taipuminen eli diffraktio ja varjostimella näkyy valoaaltojen interferenssi. \(\color{Red}{\text{(+1p)}}\)
Ratkaisu b-kohtaan
Kirjataan lähtöarvot \(\lambda=633 \text{ nm}\).
Lasketaan hilavakion suuruus.
Hilassa on 340 rakoa millimetrillä eli kahden raon välinen etäisyys on
\(d=\dfrac{0,001 \text{ m}}{340}\)
\(d \approx 2,94 \cdot 10^{-6} \text{ m}\)
Sovelletaan hilayhtälöä ja ratkaistaan varjostimella
näkyvän valomaksimin suurin kertaluku \(k\).
\(\begin{align}d \sin \alpha &= k \lambda \qquad &&||:\lambda \\ k &= \dfrac{d \sin \alpha}{\lambda}&&\color{Red}{\text{(+1p)}}\end{align} \)
\(\sin \alpha\) on suurimmillaan yksi, joten voidaan tehdä seuraava arvio.
\(\begin{align}\dfrac{d \sin \alpha}{\lambda} &\leq \dfrac{d}{\lambda} \qquad &&||k=\frac{d \sin \alpha}{\lambda}\\ k& \leq \dfrac{d}{\lambda}\end{align}\)
Sijoitetaan tunnetut lukuarvot.
\(k \leq \dfrac{2,94 \cdot 10^{-6} \text{ m}}{633 \cdot 10^{-9} \text{ m}}\)
\(k \leq 4,64\ldots\) \(\color{Red}{\text{(+1p)}}\)
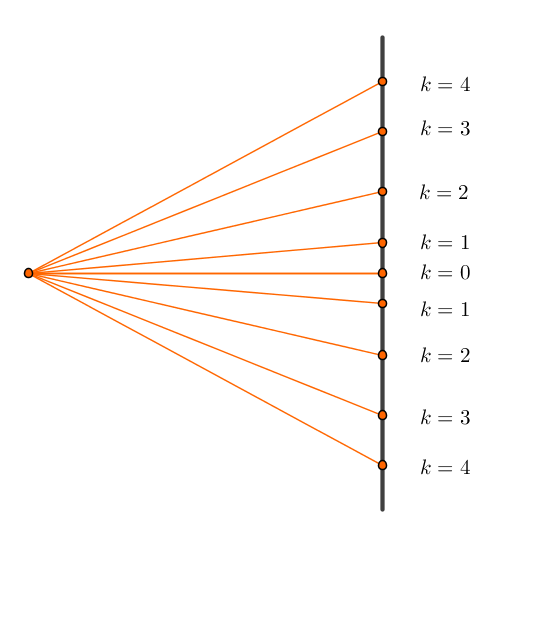
Vastaus: Varjostimelle saadaan näkyviin siis 4 + 1 + 4 valomaksimia eli yhdeksän valomaksimia. \(\color{Red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
