Sähkömagneettinen induktio ja sen sovellukset
Suljettu johdinsilmukka kulkee vakionopeudella magneettikentän läpi kuvion ohessa olevan kuvion mukaisesti.
Hahmottele ja perustele seuraavat kuvaajat:
a) silmukan magneettivuo ajan funktiona.
b) silmukkaan indusoituva jännite ajan funktiona.
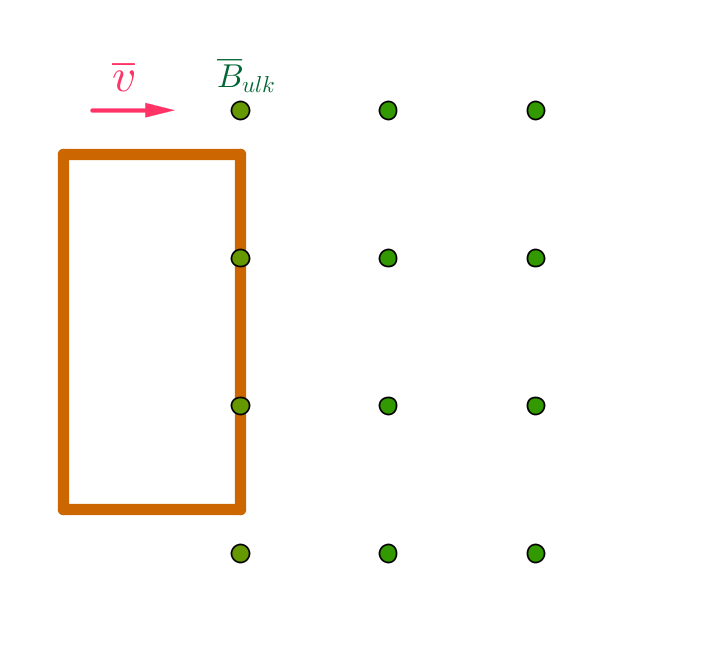
Kun magneettivuo johdinsilmukan läpi muuttuu, niin silmukkaan indusoituu induktiojännite
\(e_k = - \dfrac{\Delta \Phi}{\Delta t}\)
Magneettivuo \(\Phi\) määritellään \(\Phi = BA\), joten induktiolaki saadaan kirjoitettua muotoon:
\(\begin{align*} e_k&=-\dfrac{\Delta \Phi}{\Delta t} \\ e_k & = - \dfrac{\Delta (BA)}{\Delta t} \qquad ||\text{B ei muutu} \\ e_k & = - B \dfrac{\Delta A}{\Delta t} \end{align*}\)
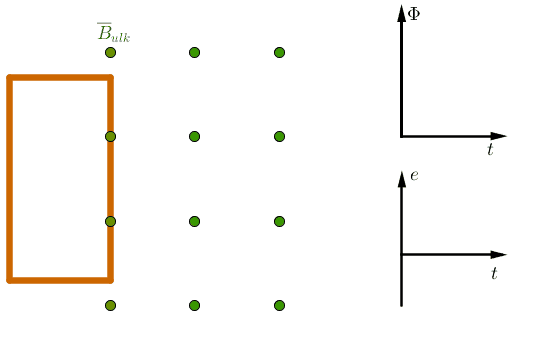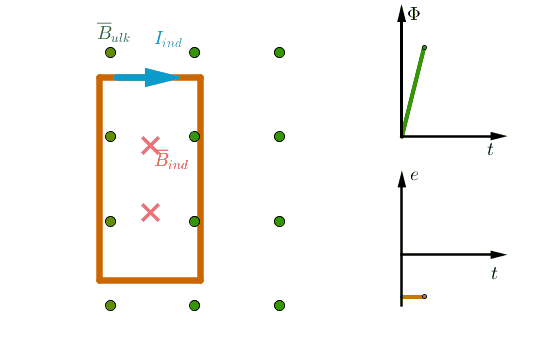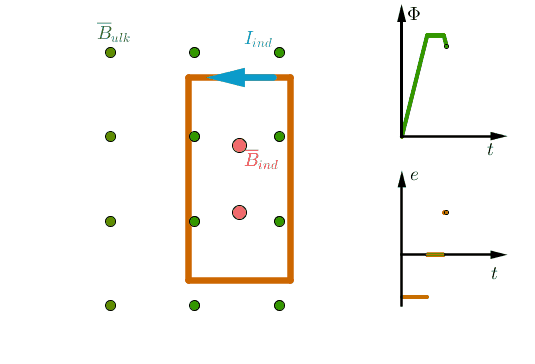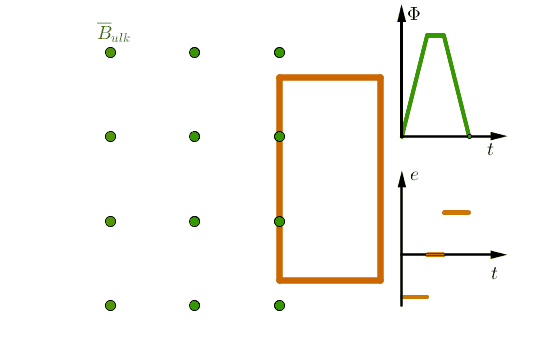
(Kuvaajien hahmotelmat oikein +3p)
1. Johdinsilmukka saapuu ulkoiseen magneettikenttään
Johdinsilmukan magneettikentässä olevan osan pinta-ala kasvaa eli \(\Delta A > 0\).
Pinta-alan kasvaessa, myös magneettivuo (\(\Phi = BA\)) kasvaa. \(\color{Red}{\text{(+0,5p)}}\)
Johdinsilmukka liikkuu vakionopeudella, joten \(\dfrac{\Delta A}{\Delta t} >0\) on vakio.
Indusoituva keskimääräinen jännite on lukuarvoltaan negatiivinen ja sen suuruus ei muutu. \(\color{Red}{\text{(+0,5p)}}\)
2. Johdinsilmukka on kokonaan ulkoisessa magneettikentässä
Johdinsilmukan magneettikentässä olevan osan pinta-ala ei kasva eli \(\Delta A = 0\).
Koska pinta-ala ei muutu, niin magneettivuo (\(\Phi = BA\)) ei muutu. \(\color{Red}{\text{(+0,5p)}}\)
Koska magneettivuo ei muutu, niin induktiojännitettä (\(e_k = - \dfrac{\Delta \Phi}{\Delta t}\)) ei indusoidu. \(\color{Red}{\text{(+0,5p)}}\)
3. Johdinsilmukka poistuu ulkoisesta magneettikentästä.
Johdinsilmukan magneettikentässä olevan osan pinta-ala pienenee eli \(\Delta A < 0\).
Pinta-alan pienentyessä, myös magneettivuo (\(\Phi = BA\)) pienenee. \(\color{Red}{\text{(+0,5p)}}\)
Johdinsilmukka liikkuu vakionopeudella, joten \(\dfrac{\Delta A}{\Delta t} <0\) on vakio.
Indusoituva keskimääräinen jännite on lukuarvoltaan positiivinen ja sen suuruus ei muutu. \(\color{Red}{\text{(+0,5p)}}\)
a) Mitä tarkoittaa itseinduktio? (2p)
b- ja c-kohta liittyvät oheiseen videoon.
b) Piirrä videolla näkyvä kytkentäkaavio. (1p)
c) Videolla näkyvän käämin läpi kulkee 3,5 ampeerin sähkövirta, joka pienenee 15 millisekunnissa arvoon 0 ampeeria.
Samalla havaitaan, että 100 voltin jännitteen vaativa hehkulamppu välähtää.
Kuinka suuri on käämin induktanssi vähintään? Käämin resistanssi voidaan olettaa pieneksi. (3p)
Ratkaisu a-kohtaan
Itseinduktiossa johtimessa oleva muuttuva sähkövirta indusoi samaan johtimeen (+1p)
sähkövirran muutosta vastustavan jännitteen (+1p).
Ratkaisu b-kohtaan
Piirretään kytkentäkaavio.
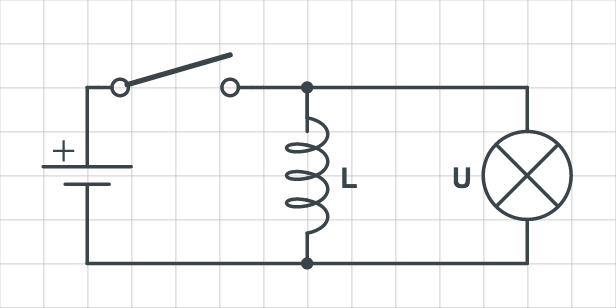
(Kytkentäkaavio oikein +1p)
Ratkaisu c-kohtaan
Oletetaan käämin ja johdinten resistanssi pieneksi.
Itseinduktiojännite on yhtä suuri, kuin lampussa tapahtuva jännitehäviö (Kirchhoffin 2. laki).
Itseinduktiojännite on vähintään 100 volttia, koska hehkulamppu välähtää. \(\color{Red}{\text{(+1p)}}\)
Keskimääräinen itseinduktiojännite saadaan suureyhtälöstä:
\(e_ k = - L \dfrac{\Delta I}{\Delta t}\). \(\color{Red}{\text{(+1p)}}\)
Ratkaistaan tästä käämin induktanssi \(L.\)
\(\begin{align*} e_ k &= - L \dfrac{\Delta I}{\Delta t} \qquad&& || \cdot \Delta t \\ e_k \Delta t & = -L \Delta I &&|| : \Delta I \\ e_k \dfrac{\Delta t}{\Delta I}&= - L &&|| \cdot (-1) \\ -e_k \dfrac{\Delta t}{\Delta I}&= L \end{align*}\)
Sijoitetaan tunnetut suureet.
\(\begin{align*} L&=-e_k \dfrac{\Delta t}{\Delta I} \\ L&=-100 \text{ V} \cdot \dfrac{0,015 \text{ s}}{-3,5 \text{ A}} \\ L& \approx 0,43 \text{ H} \end{align*}\)
Vastaus: Käämin induktanssi on vähintään 0,43 H. \(\color{Red}{\text{(+1p)}}\)
Miksi magneetin putoaminen kupariputken läpi kestää kauemmin kuin teräskuulan?
Perustele vastauksesi mahdollisimman tarkasti.
Magneetti on tasaisesti kiihtyvässä liikkeessä.
Tehtävässä riittää tilanteen tarkastelu magneetin ylä- tai alapuolelta.
Tilanne magneetin yläpuolelta katsottuna
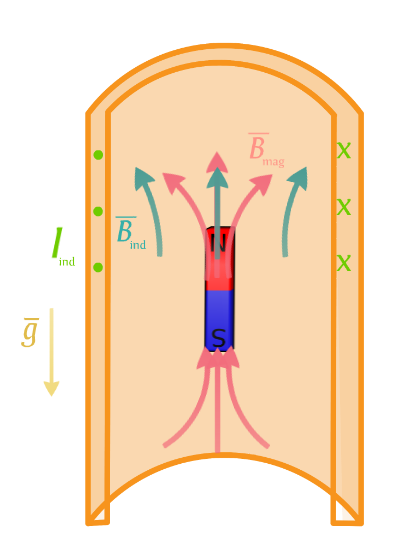
- Kestomagneetin kupariputken yläosan läpäisevä magneettikenttä heikkenee. \(\color{Red}{\text{(+1p)}}\)
- Heikkenevä magneettikenttä indusoi kupariputkeen induktiovirran. \(\color{Red}{\text{(+1p)}}\)
- Lenzin lain mukaan induktiovirran suunta on sellainen, että sen aiheuttama magneettikenttä pyrkii vastustamaan ulkoisen magneettikentän muutosta. \(\color{Red}{\text{(+2p)}}\)
- Induktiovirran magneettikenttä pyrkii ylläpitämään kestomagneetin magneettikenttää. \(\color{Red}{\text{(+1p)}}\)
- Induktiovirran magneettikenttä välittää magneettiin voiman, joka hidastaa magneetin putoamista. \(\color{Red}{\text{(+1p)}}\)
Tilanne magneetin alapuolelta katsottuna
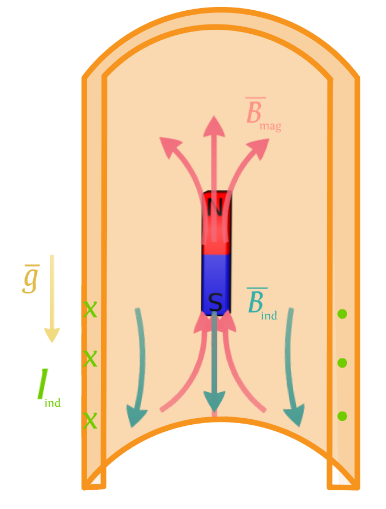
- Kestomagneetin kupariputken alaosan läpäisevä magneettikenttä voimistuu. \(\color{Red}{\text{(+1p)}}\)
- Voimistuva magneettikenttä indusoi kupariputkeen induktiovirran. \(\color{Red}{\text{(+1p)}}\)
- Lenzin lain mukaan induktiovirran suunta on sellainen, että se pyrkii vastustamaan ulkoisen magneettikentän muutosta. \(\color{Red}{\text{(+2p)}}\)
- Induktiovirran magneettikenttä pyrkii heikentämään kestomagneetin magneettikenttää. \(\color{Red}{\text{(+1p)}}\)
- Induktiovirran magneettikenttä välittää magneettiin voiman, joka hidastaa magneetin putoamista. \(\color{Red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
