a) Ratkaise kulman ß suuruus. Perustele vastauksesi.
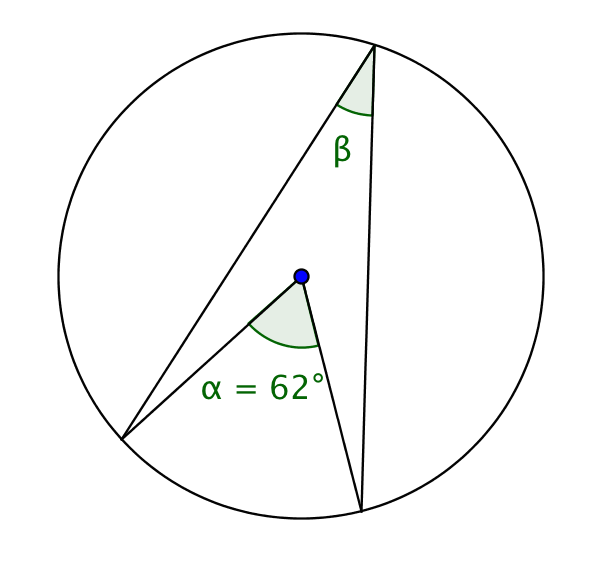
b) Kehäkulman suuruus on 120°. Määritä samaa kaarta vastaavan keskuskulman suuruus.
Merkitse vihkoosi värikynällä puuttuvat välivaiheet ja pisteet.
a) Samaa kaarta vastaava kehäkulma on puolet vastaavasta keskuskulmasta (+1p.)
Joten:
\(\beta = 62 ^ \circ : 2=31 ^ \circ\)
(lasku +1p., vastaus +1p.)
b) Keskuskulma on kaksi kertaa niin suuri kuin vastaava kehäkulma. (+1p.)
Joten:
\(2 \cdot 120 ^\circ=240^\circ\)
(lasku + 1p., vastaus +1p.)
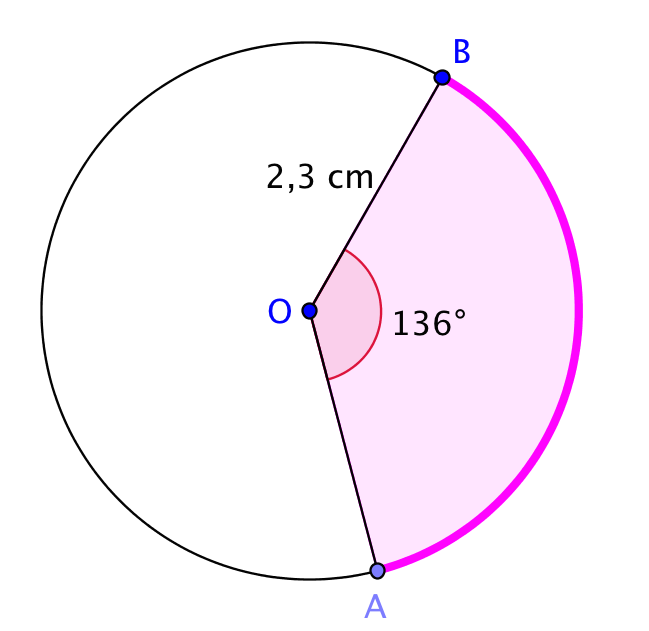
Laske kuvan sektorin
a) pinta-ala
b) kaaren pituus.
Merkitse vihkoosi värikynällä puuttuvat välivaiheet ja pisteet.
a) \(p = \frac{\alpha}{360^\circ} \cdot\pi r^2 = \frac{136 ^\circ}{360^\circ} \cdot \pi\cdot (2,3\ \text{cm})^2 \approx 6,3\ \text{cm}^2\)
(kaava +1p., lasku +1p., vastaus +1p.)
b) \(p = \frac{\alpha}{360^\circ} \cdot2\pi r = \frac{136 ^\circ}{360^\circ} \cdot2 \cdot \pi\cdot2,3 \ \text{cm} \approx 5,5\ \text{cm}\)
(kaava +1p., lasku +1p., vastaus +1p.)
Kuvassa olevan neliön sisään on piirretty suurin mahdollinen ympyrä. Laske väritetyn alueen pinta-ala.

Merkitse vihkoosi värikynällä puuttuvat välivaiheet ja pisteet.
Lasketaan ensin neliön pinta-ala:
\(A_\text{neliö}=a \cdot h =5,8 \ \text{cm} \cdot 5,8 \ \text{cm} = 33,64 \ \text{cm}^2 \) (lasku +1p., vastaus +1p.)
Lasketaan sitten ympyrän pinta-ala:
Väritetyn alueen pinta-ala saadaan, kun neliön pinta-alasta vähennetään ympyrän pinta-ala:
\(A_\text{neliö}-A_\text{ympyrä}=33,64 \ \text{cm}^2- 26,420...\ \text{cm}^2 \approx 7,2 \ \text{cm}^2\) (+1p.)
Vastaus: Väritetyn alueen pinta-ala on 7,2 cm².
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
