RL-piiri koostuu sarjaan kytketyistä vastuksesta ja käämistä.
RL-piiri kytkettiin 20 V tasajännitteeseen, jolloin piirissä kulki 4,0 A sähkövirta.
Kun RL-piiri kytkettiin 35 V vaihtojännitteeseen, niin piirissä kulki 1,5 A sähkövirta.
Vaihtovirtapiirin taajuus on 50 Hz.
a) Kuinka suuri oli RL-piirin impedanssi? (2p)
b) Kuinka suuri oli RL-piirin induktanssi? (4p)
Ratkaisu a-kohtaan
Kirjataan lähtöarvot.
\(U_1=20 \text{ V}, \ I_1=4,0 \text{ A} \\ U_2= 35 \text{ V}, \ I_2=1,5 \text{ A} \\ f=50 \text{ Hz}\)
Tarkastellaan tilannetta, jossa piiriin on kytketty tasajännite.
Oletetaan, että käämi on ideaalikäämi jolloin käämin resistanssi on nolla.
Tarkastellaan tilannetta, jossa piiriin on kytketty vaihtojännite.
Ohmin lain avulla saadaan laskettua vaihtovirtapiirin impedanssi.
\(\begin{align*}U_2&=ZI_2 \\ Z&=\dfrac{U_2}{I_2}\qquad \color{Red}{\text{(+1p)}} \end{align*}\)
Sijoitetaan tunnetut lukuarvot
\(\begin{align*} Z&=\dfrac{35 \text{ V}}{1,5 \text{ A}} \\ Z& \approx 23,33 \ \Omega \end{align*}\)
Vastaus: Vaihtovirtapiirin impedanssi on noin \(23 \ \Omega\) \(\color{Red}{\text{(+1p)}}\)
Ratkaisu b-kohtaan
Lasketaan Ohmin lain avulla RL-piirin vastuksen resistanssi.
\(\begin{align*}U_1&=RI_1 \\ R&=\dfrac{U_1}{I_1} \end{align*}\)
Sijoitetaan tunnetut lukuarvot.
\(\begin{align*} R&=\dfrac{20 \text{ V}}{4,0 \text{ A}} \\ R&=5,0 \ \Omega \qquad \color{Red}{\text{(+1p)}}\end{align*}\)
\(Z=\sqrt{R^2+(X_L - X_C)^2}\).
Koska piirissä on vain vastus ja käämi, niin impedanssi saa muodon
\(Z=\sqrt{R^2+X_L^2}\)
Ratkaistaan induktiivinen reaktanssi.
\(\begin{align*} Z&=\sqrt{R^2+X_L^2} \quad &&||( \ \ )^2 \\ Z^2&=R^2+X_L^2 \\ Z^2-R^2&=X_L^2 &&|| \sqrt{} \\ X_L&=\sqrt{Z^2-R^2} &&\color{Red}{\text{(+1p)}} \\ X_L&=\sqrt{(23,33 \ \Omega)^2 - (5,0 \ \Omega)^2} \\ X_L & \approx 22,79 \ \Omega \end{align*}\)
Käämin induktiivinen reaktanssi määritellään \(X_L = 2 \pi f L\). \(\color{Red}{\text{(+1p)}}\)
Ratkaistaan nyt käämin induktanssi \(L.\)
\(\begin{align*} X_L &= 2 \pi f L \qquad ||:2 \pi f \\ L&=\dfrac{X_L}{2 \pi f} \\ L&=\dfrac{22,79 \ \Omega}{2 \pi \cdot 50 \text{ Hz}} \\ L& \approx 0,0726 \text{ H}\end{align*}\)
Vastaus: Käämin induktanssi on noin 73 mH. \(\color{Red}{\text{(+1p)}}\)
Tietokonepohjaisen mittausjärjestelmän avulla tutkittiin vastuksessa tapahtuvaa jännitehäviötä ja vastuksen läpi kulkevaa virtaa, kun vastus oli kytketty vaihtojännitteeseen.
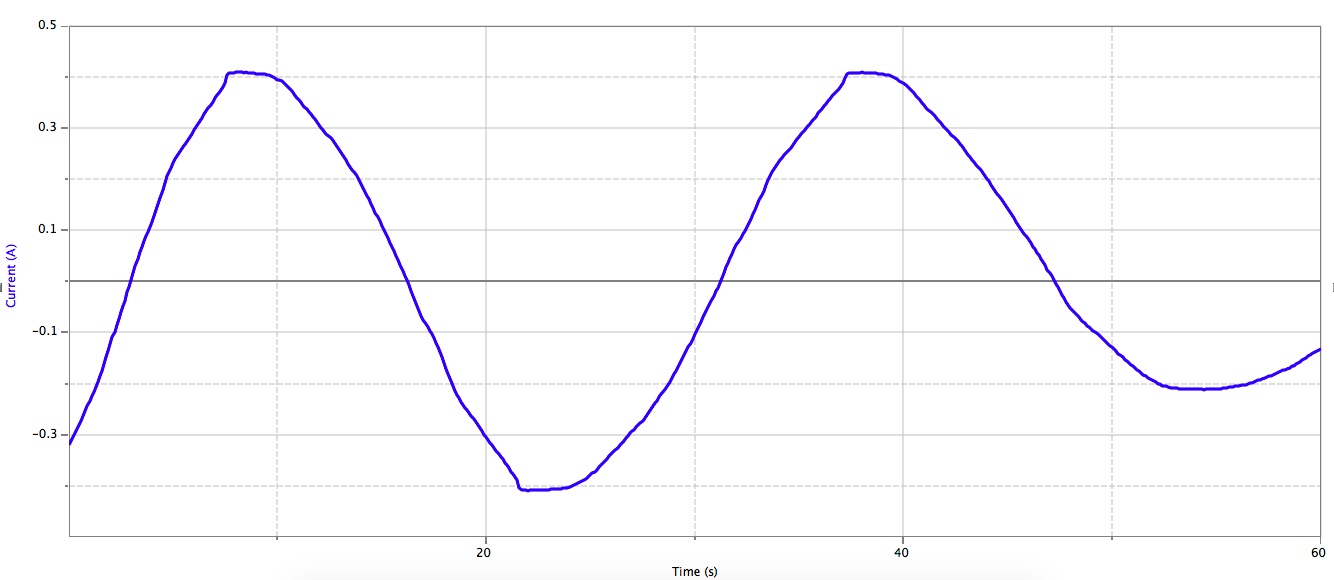
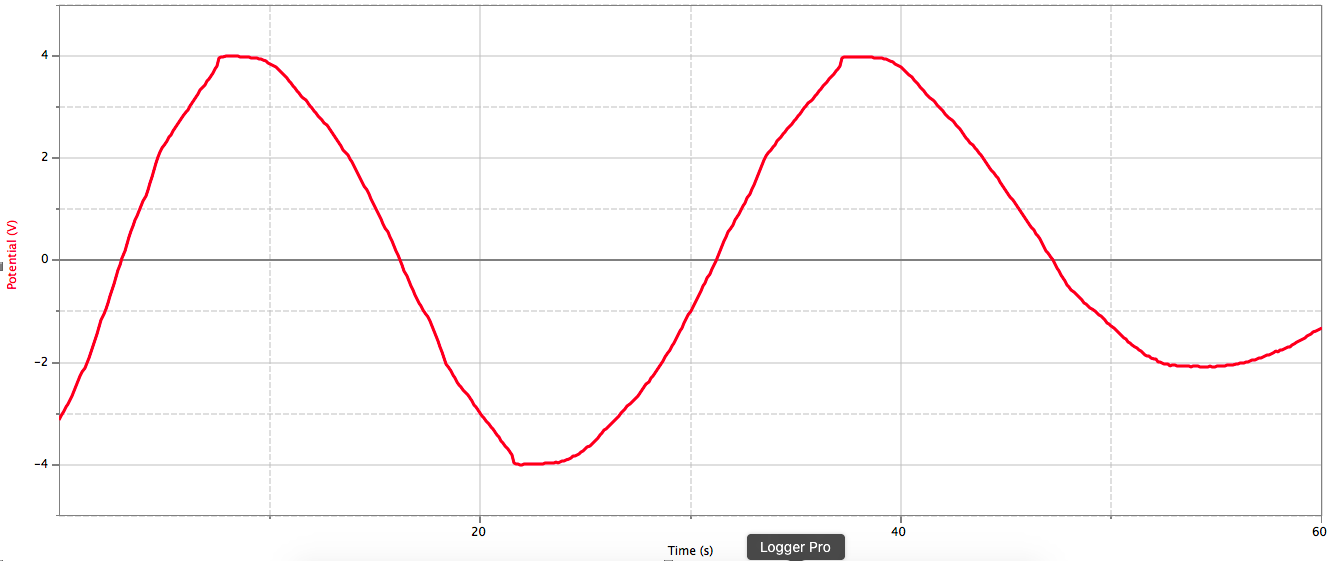
Mittauksesta saatiin oheinen kuvaaja, jossa jännitehäviö on merkitty punaisella ja vastuksen läpi kulkeva virta sinisellä.
a) Piirrä kytkentäkaavio (1p)
b) Kuinka suuri on vastuksessa tapahtuvan jännitehäviön tehollinen arvo? (1p)
c) Kuinka suuri on vastuksen läpi kulkevan sähkövirran tehollinen arvo? (1p)
d) Kuinka suuri on kytkennässä käytetyn vastuksen resistanssi? (1p)
e) Kuvaile miten virran kuvaaja muuttuu, jos vastuksen tilalle kytketään
- käämi (1p)
- kondensaattori (1p)
Ratkaisu a-kohtaan
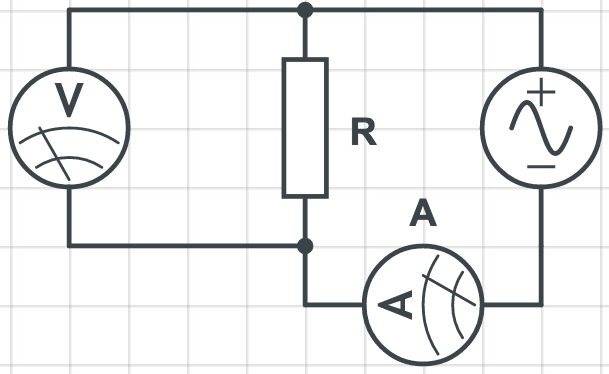 \(\color{Red}{\text{(+1p)}}\)
\(\color{Red}{\text{(+1p)}}\)
Ratkaisu b-kohtaan

Kuvaajasta saadaan luettua, että jännitehäviön huippuarvo on noin \(u_0 \approx 4,0 \text{ V}\)
Tehollinen arvo saadaan laskettua kaavalla \(U=\dfrac{u_0}{\sqrt{2}}\).
\(\begin{align*} U&=\dfrac{4,0 \text{ V}}{\sqrt{2}} \\ U& \approx 2,8 \text{ V} \qquad \color{Red}{\text{(+1p)}}\end{align*}\)
Ratkaisu c-kohtaan

Kuvaajasta saadaan luettua, että virran huippuarvo on noin \(i_0 \approx 0,41 \text{ A}\)
Tehollinen arvo saadaan laskettua kaavalla \(I=\dfrac{i_0}{\sqrt{2}}\).
\(\begin{align*} I&=\dfrac{0,41 \text{ A}}{\sqrt{2}} \\ I& \approx 0,29 \text{ A}\qquad \color{Red}{\text{(+1p)}}\end{align*}\)
Ratkaisu e-kohtaan
Käämissä tapahtuvan itseinduktion takia sähkövirta on jännitehäviötä jäljessä.
Sähkövirta saavuttaa huippunsa vasta jännitehäviön huipun jälkeen. \(\color{Red}{\text{(+0,5p)}}\)
Sähkövirran huippuarvo myös muuttuisi, koska piirin impedanssi muuttuu. \(\color{Red}{\text{(+0,5p)}}\)
Kun kondensaattori on täysin varautunut, niin levyjen välinen jännitehäviö on suurimmillaan ja sähkövirta on nolla.
Tämän takia Sähkövirta saavuttaa huippunsa ennen jännitehäviön huippua. \(\color{Red}{\text{(+0,5p)}}\)
Sähkövirran huippuarvo myös muuttuisi, koska piirin inpedanssi muuttuu. \(\color{Red}{\text{(+0,5p)}}\)
Teholtaan 1,7 kW:n tehosekoitin on kytketty 230 V sähköverkkoon.
Tehosekoittimen jännitehäviön ja sähkövirran välinen vaihe-ero on \(25^{\circ}.\)
Laske tehosekoittimen ottaman sähkövirran huippu- ja tehollisarvot.

Kirjataan lähtöarvot.
\(U=230\text{ V}, \ P=1700 \text{ W}, \ \varphi = 25^{\circ}\)
Teho, jonka tehosekoitin ottaa vaihtovirtaverkosta on
\(P=UI \cos \varphi\). \(\color{Red}{\text{(+1p)}}\)
Ratkaistaan sähkövirran tehollinen arvo \(I\).
\(\begin{align*}P&=UI \cos \varphi \qquad &&||:U \cos \varphi \\ I&=\dfrac{P}{U \cos \varphi} && \color{Red}{\text{(+1p)}} \end{align*}\)
Sijoitetaan tunnetut lukuarvot.
\(I = \dfrac{1700 \text{ W}}{230 \text{ V} \cdot \cos 25^{\circ}} \qquad \qquad \color{Red}{\text{(+1p)}} \\ I \approx 8,16 \text{ A }\)
Lasketaan sähkövirran huippuarvo.
\(\begin{align*}I&=\dfrac{i_0}{\sqrt{2}} \qquad \qquad \color{Red}{\text{(+1p)}} \\ i_0 &= \sqrt{2} I\\ i_0& = \sqrt{2} \cdot 8,16 \text{ A } \\ i_0 &\approx 11,5 \text{ A} \end{align*}\)
Vastaus: Sähkövirran huippuarvo on noin 12 A ja tehollinen arvo noin 8,2 A. \(\color{Red}{\text{(+2p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
