FY8 t1.1

Suositeltava osaamistaso: 
80%

a) Mikä on Planckin kvanttihypoteesi? 

b) Mitä tarkoittaa Einsteinin valon kvanttiteoria?

c) Valon aallonpituus on 600 nm. Laske yhden fotonin 

  • energia
  • liikemäärä

 

 

Pisteytysohje: 

Ratkaisu a-kohtaan.

  • Aine luovuttaa ja ottaa vastaan säteilynä vain tietynsuuruisina energiapaketteina eli kvantteina. \( \color{Red}{\text{(+1p)}}\)
  • Kvantin energia on E=hf, jossa f on säteilyn taajuus ja h Planckin vakio.\( \color{Red}{\text{(+1p)}}\)

Ratkaisu b-kohtaan.

  • Sähkömagneettinen säteily koostuu kvanteista, joita kutsutaan fotoneiksi. \( \color{Red}{\text{(+1p)}}\)
  • Fotonin nopeus on valon nopeus, fotoni on massaton ja sähköisesti neutraali hiukkanen.\( \color{Red}{\text{(+1p)}}\)
Ratkaisu c-kohtaan.
Kirjataan lähtöarvot.
$\lambda=600 \cdot 10^{-9} \text{ m}, \ , c=2,99792458 \cdot 10^8 \text{ m/s}, \\ h=6,6260755 \cdot 10^{-34} \text{ Js}=4,135669 \cdot 10^{-15} \text{ eVs}$
 
Fotonin energia saadaan kaavalla $E=hf$ ja liikemäärä kaavalla $p=\dfrac{h}{\lambda}$.
 
Lasketaan fotonin energia.
 
\(\begin{align*} E&=hf \qquad &&||c=\lambda f \\ E&=\dfrac{h c}{\lambda} &&\color{Red}{\text{(+0,5p)}} \\ E&=\dfrac{6,6206755 \cdot 10^{-34} \text{ Js} \cdot 2,99792458 \cdot 10^8 \text{ m/s}}{600 \cdot 10^{-9}\text{ m}} && (*) \\ E& \approx 3,308 \cdot 10^{-19} \text{ J}\end{align*}\)
 
tai
 
\(\begin{align*} E&=\dfrac{4,135669 \cdot 10^{-15} \text{ eVs} \cdot 2,99792458 \cdot 10^8 \text{ m/s}}{600 \cdot 10^{-9}\text{ m}} && (*) \\ E& \approx 2, 066 \text{ eV}\end{align*}\)
 
Lasketaan fotonin liikemäärä.
\(\begin{align*} p&=\dfrac{h}{\lambda} &&\color{Red}{\text{(+0,5p)}} \\ p&=\dfrac{6,6206755 \cdot 10^{-34} \text{ Js}}{600 \cdot 10^{-9} \text{ m}} \\ p&\approx1,103 \cdot 10^{-27} \text{ kgm/s} \end{align*}\)
 
Vastaus: Fotonin energia on noin \(2,1 \text{ eV} \ \color{Red}{\text{(+0,5p)}}\) ja liikemäärä \(1,1 \cdot 10^{-27} \text{ kgm/s} \ \color{Red}{\text{(+0,5p)}}\)
Pisteytysohjeen mukaiset pisteet
Ymmärryksen arviointi
Navigointi

a) Mitä tarkoittaa valosähköinen ilmiö? (3p)

b) Sinkin irroitustyö on 4,34 eV. Laske, mikä on suurin sähkömagneettisen säteilyn taajuus, jolla elektroni vielä irtoaa sinkin pinnasta.  

    Voit käyttää apunasi alla olevaa Java-applettia.

Pisteytysohje: 

Ratkaisu a-kohtaan

Valosähköisessä ilmiössä saadaan aikaan sähkövirta tyhjiöputkeen \(\color{Red}{\text{(+3/4p)}}\) tiettyä kynnystaajuutta suuremmilla valon taajuuksilla. \(\color{Red}{\text{(+3/4p)}}\) 

Osa säteilykvantin energiasta kuluu elektronin irrottamiseen metallista \(\color{Red}{\text{(+3/4p)}}\) ja loppu muuntuu elektronin kineettiseksi energiaksi.\(\color{Red}{\text{(+3/4p)}}\) 

Ratkaisu b-kohtaan

Kirjataan lähtöarvot

 \(W_0=4,34 \text{ eV}, \ h=4,135669 \cdot 10^{-15} \text{ eVs}\), 

Valosähköisen ilmiön energiayhtälö \(E_\text{k}^{\text{max}}=hf-W_0\). \(\color{Red}{\text{(+1p)}}\)

Rajatilanteessa, jossa elektroni juuri ja juuri irtoaa katodilta pätee \(E_{\text{k}}^{\text{max}}=0 \text{ eV}\). \(\color{Red}{\text{(+1p)}}\)

Lasketaan tämän perusteella säteilyn taajuus.

\(\begin{align*} 0&=hf-W_0 \\ hf&=W_0 &&||:h \\ f&=\frac{W_0}{h}\\ f&=\dfrac{4,34 \text{ eV}}{4,135669 \cdot 10^{-15} \text{ eVs}} \\ f& \approx 1,05 \cdot 10^{15} \end{align*}\)

Vastaus: Säteilyn taajuus on noin. 1,05 PHz. \(\color{Red}{\text{(+1p)}}\)

Pisteytysohjeen mukaiset pisteet
Ymmärryksen arviointi
Navigointi

a) Miten röntgensäteily syntyy?

b) Röntgenputken kiihdytysjännite oli 60 kV. Laske syntyvän röntgensäteilyn lyhin aallonpituus.

Pisteytysohje: 

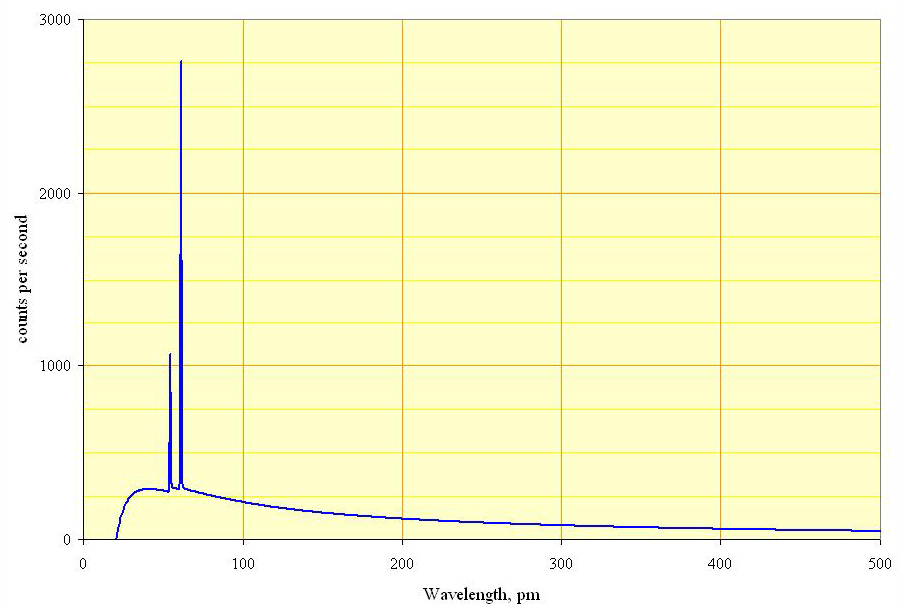
Ratkaisu a-kohtaan

  • Röntgensäteilyä syntyy muun muassa nopeiden elektronien törmätessä metallikohtioon.  (+1p)
  • Jarrutussäteilyssä elektronin liike-energia muuntuu röntgensäteilyn liike-energiaksi.  (+1p)
  • Röntgenputken ominaissäteilyn aallonpituudet riippuvat röntgenputken anodiaineesta.  (+1p)

Ratkaisu b-kohtaan

Kirjataan lähtöarvot 

\(U = 60 \ 000 \text{ V}, \ q=1 \text{ e}, \ h=4,135669 \cdot 10^{-15}\text{ eVs} \\ c=2,99792458 \cdot 10^8 \text{ m/s}\)

Elektroni kiihdytetään sähkökentässä, jolloin sähkökentän tekemä työ on $W=qU$.

Tehty työ on yhtä suuri kuin elektronin liike-energia $W=E_k=\dfrac{1}{2}mv^2$.

Elektroni luovuttaa koko liike-energiansa yhdelle röntgenkvantille $E_k = hf_\text{max}$. (+1p)

Nyt saadaan ratkaistua syntyvän röntgensäteilyn lyhin aallonpituus.

\(\begin{align*} qU&=hf_{\text{max}} \\ qU&=\dfrac{hc}{\lambda_{\text{min}}} \qquad \color{Red}{\text{(+1p)}}\\ qU\lambda_{\text{min}}&=hc \\ \lambda_{\text{min}}&=\dfrac{hc}{qU} \\ \lambda_{\text{min}}&=\dfrac{4,135669 \cdot 10^{-15} \text{ eVs}\cdot 2,99792458 \cdot 10^8 \text{ m/s}}{1 \text{ e} \cdot 60 \ 000 \text{ V}} \\ \lambda_{\text{min}} &\approx 21 \text{ pm} \end{align*}\)

Vastais: 21 pm (+1p)

 

Pisteytysohjeen mukaiset pisteet
Ymmärryksen arviointi
Navigointi

Tekemäsi itsearvion pohjalta tuloksesi prosentteina on: