Polynomifunktio ja muutosnopeus
Olkoon funktio $f(x)=x^2+3x-4$.
a) Laske funktion $f$ arvo, kun $x=-2$.
b) Ratkaise, millä $x$:n arvoilla $f(x)=14$.
c) Ratkaise piirtämällä, missä pisteissä $f$ leikkaa koordinaattiakselit.
b) Ratkaise laskemalla, missä pisteissä $f$ leikkaa koordinaattiakselit.
a)\(\begin{align} f(-2)&=(-2)^2+3\cdot (-2)-4\\ &= 4 - 6 - 4 \\ &=-6 \end{align}\) $\color{Red}{(+1\text{ p})}$
b) \(\begin{align} x^2+3x-4&=14\\ x^2+3x-4-14&=0\\ x^2+3x-18 &= 0 \end{align}\)
Toisen asteen yhtälön ratkaisukaavalla:
\(\begin{align} x& = {-3 \pm \sqrt{3^2-4\cdot 1 \cdot (-18)} \over 2\cdot 1} \\ &=\frac{-3 \pm \sqrt{9+72}}{2} \\ &= \frac{-3 \pm \sqrt{81}}{2} \\ &= \frac{-3 \pm 9}{2} \end{align}\)
\(\begin{align} x&=\frac{-3+9}{2} \\ &=\frac{6}{2} \\ &= 3 \end{align}\) tai \(\begin{align} x&=\frac{-3-9}{2}\\ &=\frac{-12}{2} \\ &=-6 \end{align}\)
Vastaus: $x=-6$ tai $x=3$ $\color{Red}{(+1\text{ p})}$
c) Piirretään funktio $f$ koordinaatistoon ja katsotaan, missä pisteissä se leikkaa koordinaattiakselit.
Funktio $f$ leikkaa siis $x$-akselin pisteissä $(-4,0)$ ja $(1,0)$ ja $y$-akselin pisteessä $(0,4)$. $\color{Red}{(+1\text{ p})}$
d) Funktio $f(x)=x^2+3x-4$ leikkaa $x$-akselia, kun $f(x)=0$, joten ratkaistaan yhtälö
\(\begin{align} x^2+3x-4=0 \end{align}\)
\(\begin{align} x &= {-3 \pm \sqrt{3^2-4\cdot 1 \cdot (-4)} \over 2\cdot 1} \\ & = {-3 \pm \sqrt{9+16}} \over 2 \\ &= \frac{-3 \pm \sqrt{25}}{2} \\ &=\frac{-3\pm5}{2} \end{align}\)
\(\begin{align} x&=\frac{-3+5}{2} \\ &=\frac{2}{2} \\ &= 1 \end{align}\) tai \(\begin{align} x&=\frac{-3-5}{2} \\ &= \frac{-8}{2} \\ &= -4 \end{align}\)$\color{Red}{(+1\text{ p})}$
Funktio leikkaa $y$-akselin, kun $x=0$. Lasketaan siis funktion arvo, kun $x=0$:
\(\begin{align} f(0)&=0^2+3\cdot 0 -4 \\ &= 0 + 0 -4 \\ &= -4 \end{align}\)$\color{Red}{(+1\text{ p})}$
Vastaus: funktio $f$ leikkaa $x$-akselin pisteissä $(-4,0)$ ja $(1,0)$ ja $y$-akselin pisteessä $(0,-4)$ $\color{Red}{(+1\text{ p})}$
Santtu lähtee pururadalle juoksulenkille. Lenkin aikana hän pysähtyy harjoittelemaan ulkokuntosalille ja jatkaa sen jälkeen matkaa.
a) Kuinka pitkän lenkin Santtu tekee?
b) Mikä on Santun keskinopeus (km/h) ensimmäisen 20 minuutin ajan?
c) Kuinka kauan Santtu viipyy ulkokuntosalilla?
d) Kuinka pitkän matkan Santtu juoksee ulkokuntosalilla käynnin jälkeen?
e) Mikä on Santun keskinopeus (km/h) koko lenkin aikana, jos pysähdystä ulkokuntosalilla ei oteta huomioon?
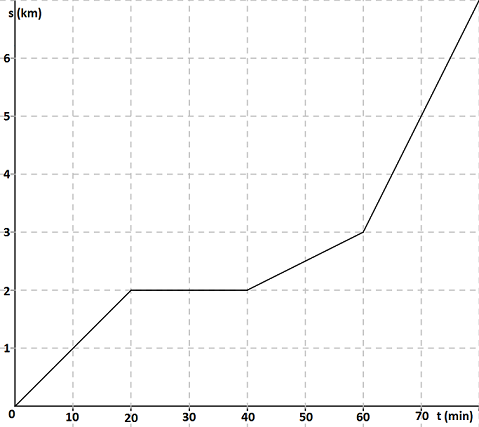
a) Lenkin pituus on 7 km. $\color{Red}{\text{(+1p)}}$
b) Santtu kulkee ensimmäisen 20 minuutin aikana 2 km. Muuten aika tunneiksi: $20\text{ min} = \frac{20}{60}\text{ h}=\frac{1}{3}\text{ h}$.
Lasketaan keskinopeus: $\frac{2 \text{ km}}{\frac{1}{3}\text{ h}}=6\text{ km/h}$. $\color{Red}{\text{(+1p)}}$
c) Santtu ei etene aikavälillä 20 - 40 min, joten hän on ulkokuntosalilla $40 \text{ min} - 20 \text{ min}=20 \text{ min}$.$\color{Red}{\text{(+1p)}}$
d) Ulkokuntosali sijaitsee 2 km päässä aloituspaikasta ja koko lenkin pituus oli 7 km, joten ulkokuntosalin jälkeen matkaa on jäljellä $7 \text{ km} - 2 \text{ km} = 5 \text{ km}$. $\color{Red}{\text{(+1p)}}$
e) Santulla menee koko lenkkiin aikaa 80 minuuttia, josta hän on pysähdyksissä 20 minuuttia. Siten Santtu juoksee $80 \text{ min}-20 \text{ min}=60 \text{ min} = 1 \text{ h}$. $\color{Red}{\text{(+1p)}}$
Koska lenkki oli 7 km pitkä, on Santun keskinopeus koko matkalla $\frac{7 \text{ km}}{1 \text{ h}}=7 \text{ km/h}$. $\color{Red}{\text{(+1p)}}$
(Tämä tehtävä suositellaan tehtäväksi tietokoneella tai tablet-laitteella.)
Tutki alla olevien liukukytkimien avulla funktion $f(x)=ax^2+bx+c$ kuvaajan muotoa muuttujien $a$, $b$ ja $c$ eri lukuarvoilla.
a) Kuvaile sanallisesti, miten muuttujien $a$, $b$ ja $c$ lukuarvon muuttaminen vaikuttaa kuvaajaan muotoon tai sijaintiin.
b) Ratkaise graafisesti (liikuttamalla punaista pistettä käyrällä) yhtälö \(3=x^2−x+1\).
c) Määritä graafisesti $f(−1)$, kun \(f(x)=−2x^2+3x+5\).
a)
- Muotoa $f(x)=ax^2+bx+c$ olevan funktion kuvaaja on paraabeli.
- Toisen asteen termin kerroin $a$ vaikuttaa paraabelin aukeamissuuntaan. Kun $a>0$, paraabeli on ylöspäin aukeava, ja kun $a<0$, paraabeli on alaspäin aukeava. \(\require{color}\color{red}\text{(+1p)}\)
- Ensimmäisen asteen termin kerroin $b$ vaikuttaa paraabelin sijaintiin sekä pysty- että sivusuunnassa. Vakiotermi $c$ vaikuttaa paraabelin sijaintiin vain pystysuunnassa. \(\require{color}\color{red}\text{(+1p)}\)
- Havaitaan, että paraabeli leikkaa $y$-akselin aina pisteessä $(0,c)$.
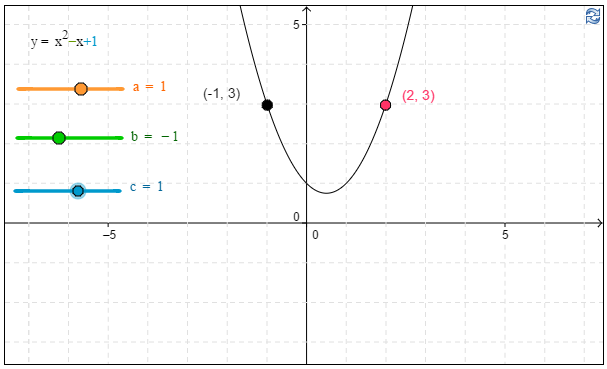
b) Kuvaajan avulla havaitaan, että yhtälön $3=x^2−x+1$ ratkaisu on \(x\approx-1\)tai \(x\approx2\). \(\require{color}\color{red}\text{(+2p)}\)
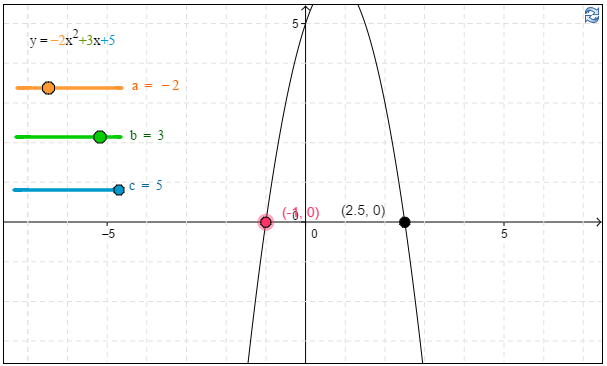
c) Kuvaajan avulla havaitaan, että funktion $f(x)=−2x^2+3x+5$ arvo \(f(-1)\approx0\). \(\require{color}\color{red}\text{(+2p)}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
