Keilapallo heitetään nopeudella 4,5 m/s keilaradalle.
Osuessaan keiloihin keilapallon nopeus pienenee arvoon 3,5 m/s.
Mikä on keilapalloon vaikuttava keskimääräinen voima, kun hidastuminen tapahtuu 70 cm matkalla?
Keilapallon massa on 6,0 kg.

Kirjataan lähtöarvot
\(v_0=4,5 \text{ m/s}, \ v_1=3,5 \text{ m/s} \\ \Delta x=0,70 \text{ m}, \ m=6,0 \text{ kg}\)
Keilapalloon kohdistuvan kokonaisvoiman tekemä työ on
yhtä suuri kuin keilapallon liike-energan muutos \(\require{color}\color{red}{\text{(+1p)}}\)
\(W=\Delta E_k\)
\(F \cdot \Delta x = \dfrac{1}{2}mv_1^2-\dfrac{1}{2}mv_0^2\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(F \cdot \Delta x = \dfrac{1}{2}m\Big(v_1^2-v_0^2\Big)\)
\(F=\dfrac{m(v_1^2-v_0^2)}{2\Delta x}\) \(\require{color}\color{red}{\text{(+2p)}}\)
Sijoitetaan lukuarvot
\(F=\dfrac{6,0 \text{ kg} ( (4,5 \text{ m/s})^2-(3,5 \text{ m/s})^2}{2 \cdot 0,70 \text{ m}}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(F \approx 34,3 \text{ N}\)
Vastaus: Keilapalloon kohdistuva keskimääräinen voima on noin 34 N. \(\require{color}\color{red}{\text{(+1p)}}\)
Haukka lentää 30 metrin korkeudella nopeudella 4,5 m/s.
Lentäessään haukka huomaa maanpinnalla nukkuvan jäniksen ja syöksyy tätä kohti.
Kuinka suuri haukan nopeus on törmäyshetkellä?

Kirjataan lähtöarvot
\(h_0 = 30 \text{ m}, \ v_0=4,5 \text{ m/s},\\ g=9,81 \text{ m/s}^2\)
Oletetaan, että mekaaninen energia säilyy
haukan syöksyn aikana. \(\require{color}\color{red}{\text{(+1p)}}\)
\(E_{aluksi}=E_{lopuksi}\)
\(E_{p0}+E_{k0}=E_{p1}+E_{k1}\)
Asetetaan potentiaalienergian nollataso jäniksen korkeudelle,
jolloin \(E_{p1}=0 \text{ J}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(mgh_0+\dfrac{1}{2}mv_0^2=\dfrac{1}{2}mv_1^2\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(gh_0+\dfrac{1}{2}v_0^2=\dfrac{1}{2}v_1^2\)
\(2gh_0 +v_0^2=v_1^2\)
\(v_1=\sqrt{2gh_0+v_0^2}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(v_1=\sqrt{2 \cdot 9,81 \text{ m/s}^2 \cdot 30 \text{ m} + (4,5 \text{ m/s}^2}\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(v_1 \approx 24,7 \text{ m/s}\)
Vastaus: Haukan nopeus törmäyshetkellä on noin 25 m/s. \(\require{color}\color{red}{\text{(+1p)}}\)
Levossa olevaa laatikkoa, jonka massa on 5,0 kg, vedetään 10 N voimalla oikealle kolmen metrin pituinen matka.
Kuinka suuri on laatikon loppunopeus, kun laatikon ja pinnan välinen liukukitkakerroin on 0,20?

Kirjataan lähtöarvot
\(m=5,0 \text{ kg}, \ F=10 \text{ N} \\ \mu = 0,20, \ \Delta x=3,0 \text{ m}\)
Piirretään voimakuvio
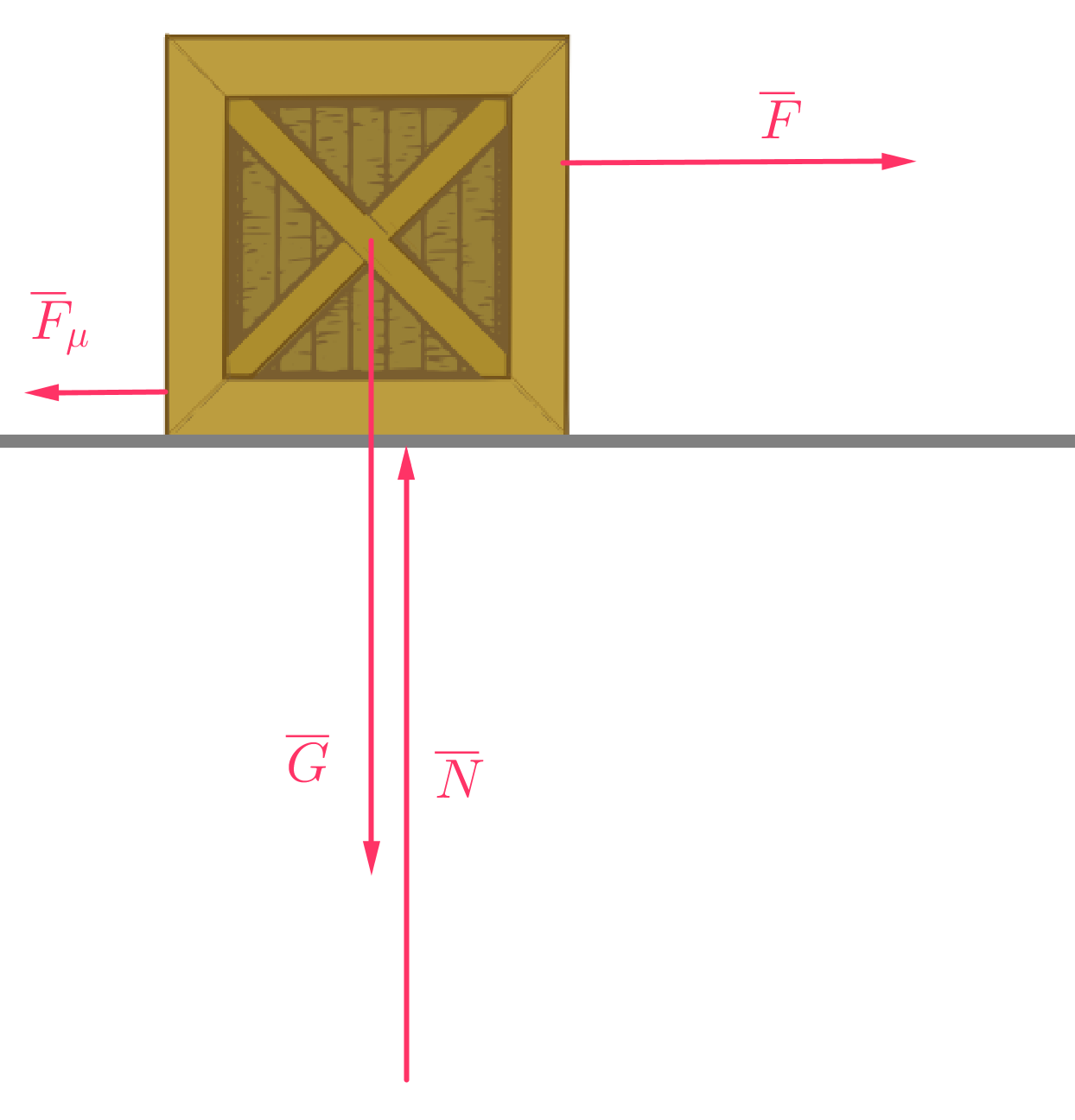
Lasketaan laatikkoon vaikuttavan kokonaisvoiman suurus.
Tehdään Newtonin 2. lain mukaiset voimatarkastelut x- ja y-suunnassa. \(\require{color}\color{red}{\text{(+1p)}}\)
\(\sum \overline{F}_y=\overline{0}\)
\(\overline{G}+\overline{N}=\overline{0}\)
\(-G+N=0\)
\(N=G\)
\(N=mg\)
x-suunnassa
\(\overline{F}_{kok}=\overline{F}+\overline{F}_\mu\)
\(F_{kok}=F-F_\mu \quad || F_\mu=\mu N\)
\(F_{kok}=F-\mu N\)
\(F_{kok}=F-\mu mg\) \(\require{color}\color{red}{\text{(+1p)}}\)
Työperiaateen mukaan kappaleeseen kohdistuva kokonaisvoima
aiheuttaa kappaleen liike-energian muutoksen. \(\require{color}\color{red}{\text{(+1p)}}\)
\(W=\Delta E_k\)
\(F_{kok}\Delta x=\dfrac{1}{2}mv_1^2-\dfrac{1}{2}mv_0^2\)
\(F_{kok}\Delta x=\dfrac{1}{2}mv_1^2\) \(\require{color}\color{red}{\text{(+1p)}}\)
\(2F_{kok}\Delta x=mv_1^2\)
\(v_1=\sqrt{\dfrac{2F_{kok}\Delta x}{m}}=\sqrt{\dfrac{2(F-\mu mg)\Delta x}{m}}\)
\(v_1=\sqrt{\dfrac{2 \cdot (10 \text{ N}-0,2 \cdot 5,0 \text{ kg} \cdot9.81 \tfrac{\text{m}}{\text {s}^2}) \cdot 3,0 \text{ m}}{5,0 \text{ kg}}}\)\(\require{color}\color{red}{\text{(+1p)}}\)
\(v_1=0,477... \text{ m/s} \approx 0,48 \text{ m/s}\)
Vastaus: Laatikon loppunopeus on noin 0,48 m/s \(\require{color}\color{red}{\text{(+1p)}}\)
Tekemäsi itsearvion pohjalta tuloksesi prosentteina on:
